그래스호퍼 상의 여러 Parameter와 명령어를 이용하여 만든 Parametric Tower이다.

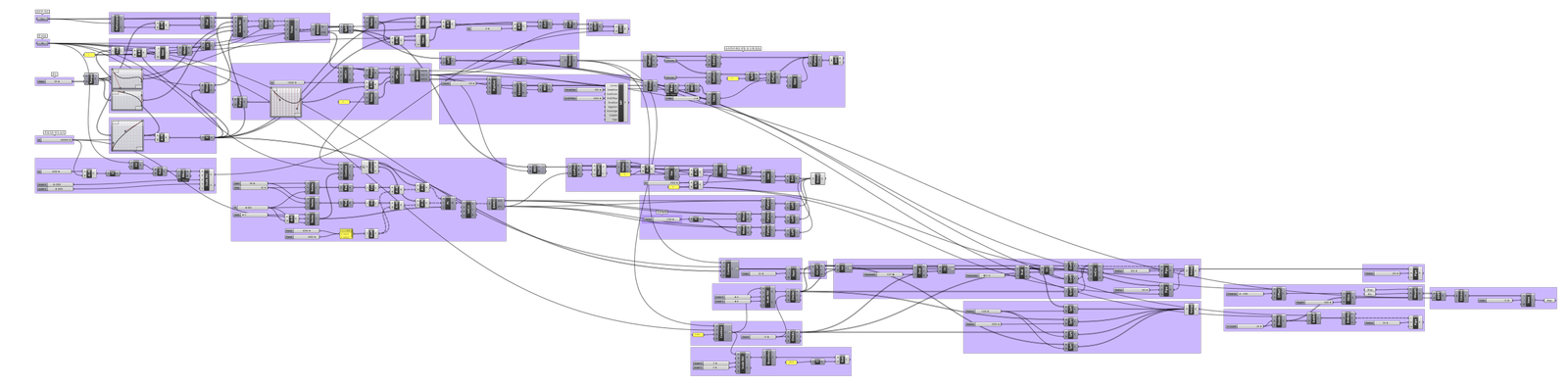
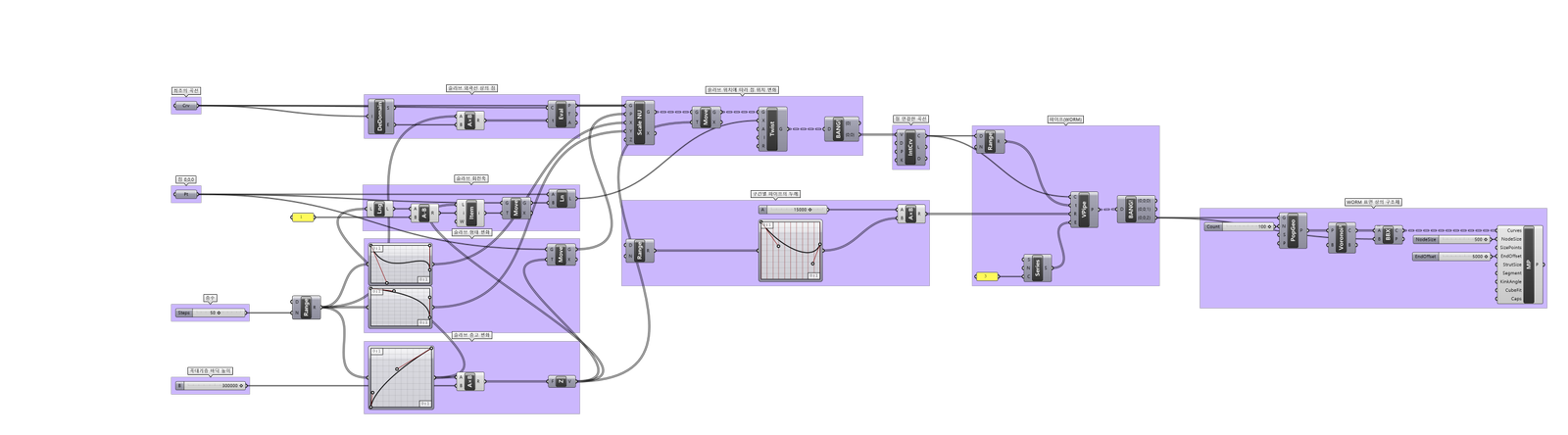
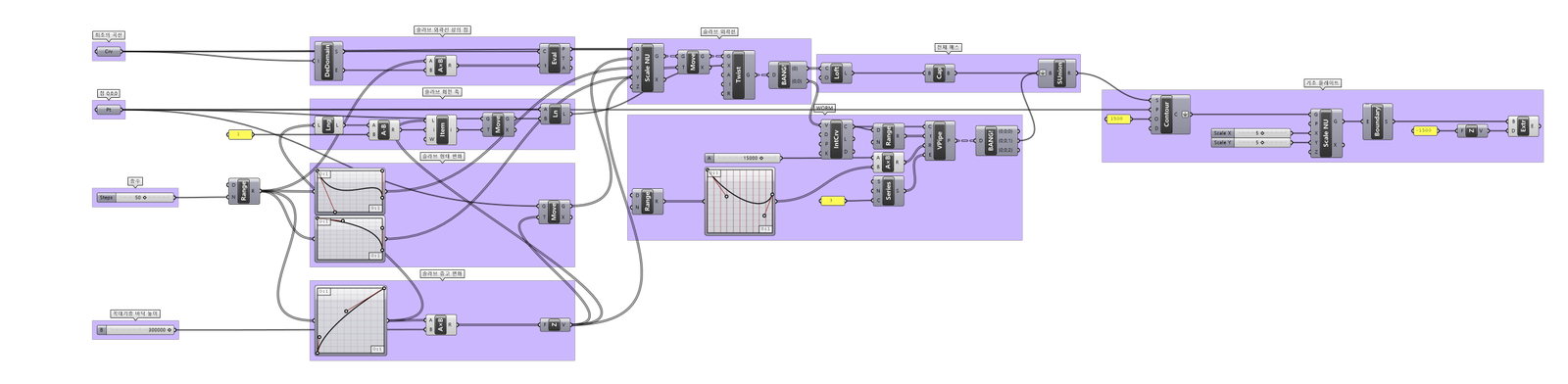
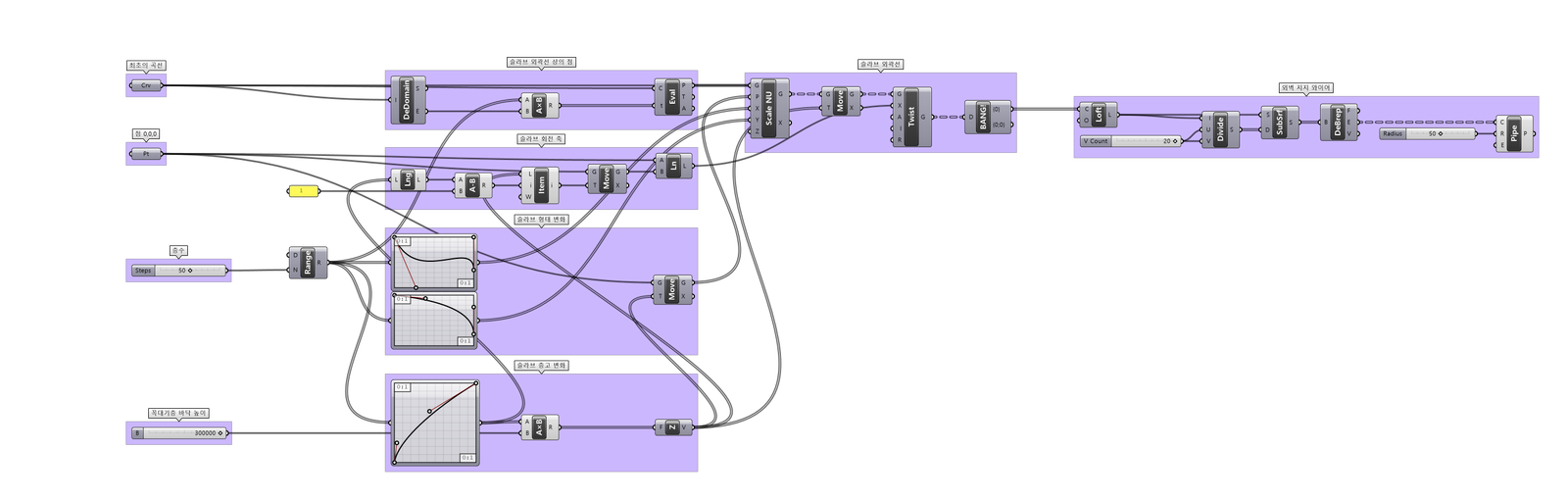
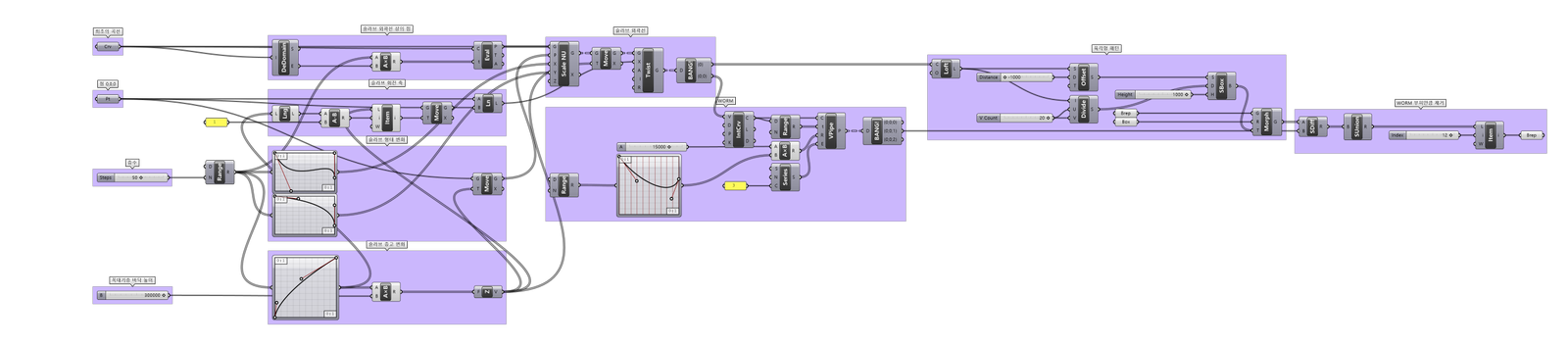
Parametric Tower를 구현하는 데에 사용된 그래스호퍼 알고리즘이다.

간단한 디자인 프로세스이며 코어 -> 슬라브 -> 지렁이(추후 자세한 설명) -> 계단 -> 기초 -> 지지 와이어 -> 파사드의 패턴 순으로 진행하였다.

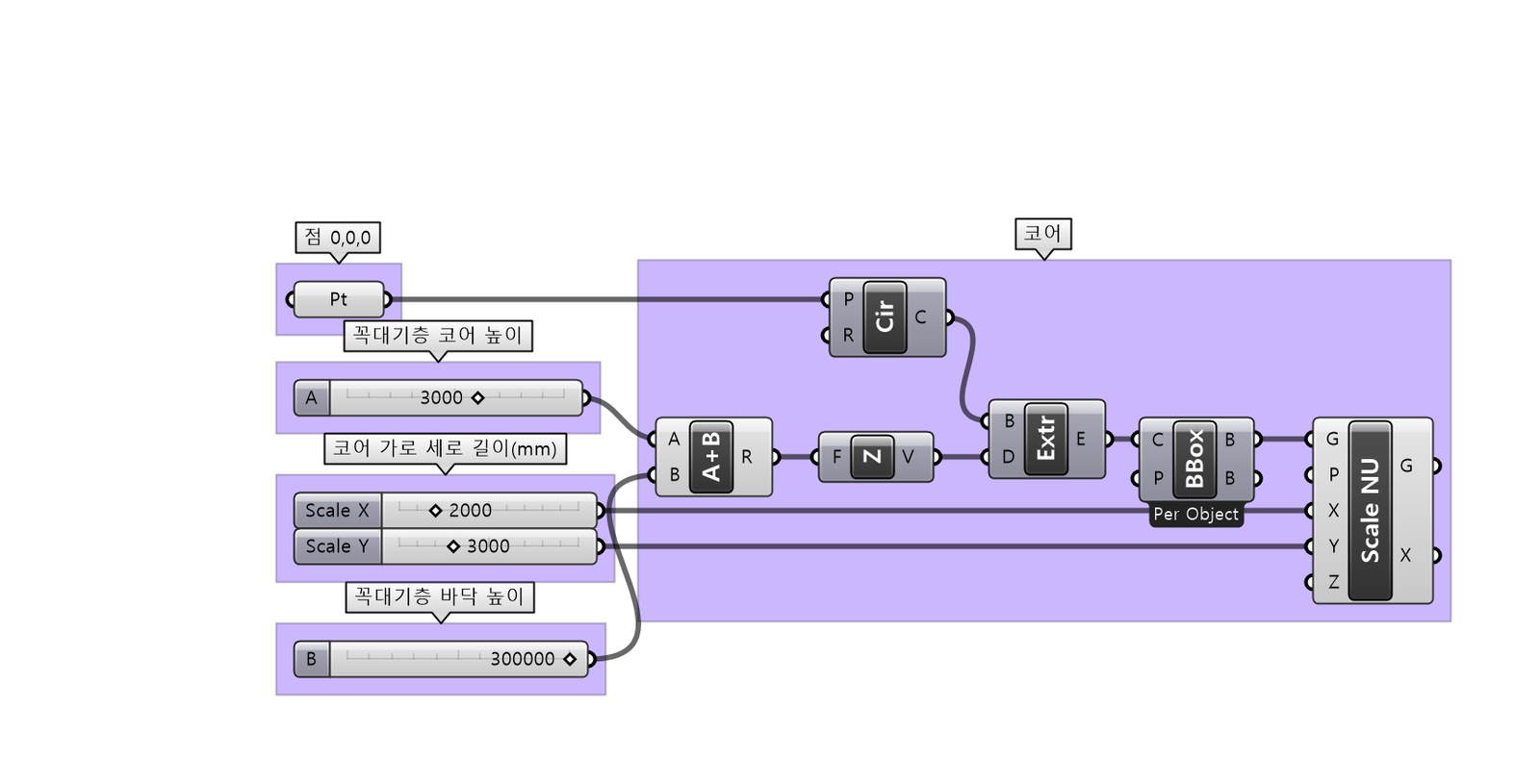
1. Core 타워의 코어이다. 1) 단순한 박스형태이기 때문에 간단한 알고리즘으로 완성했다.

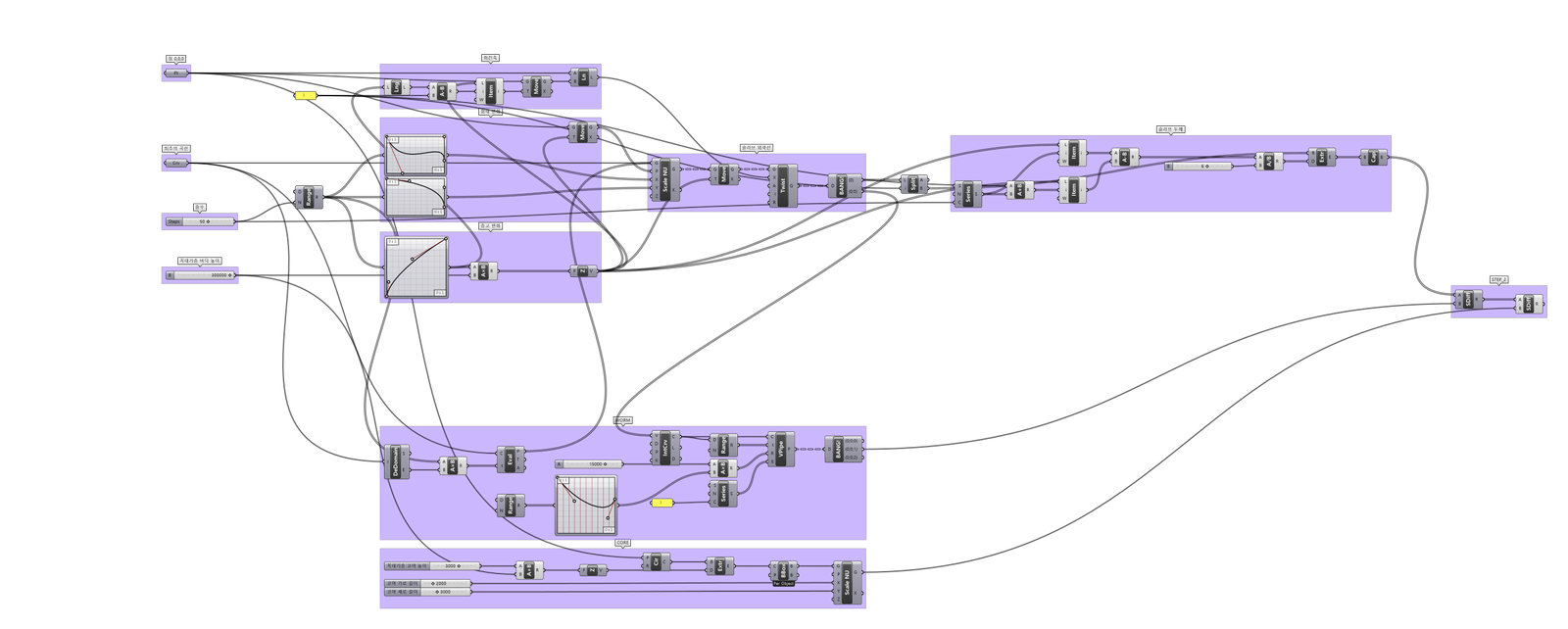
2. Slab 각 층의 슬라브이다. 1) 바닥에 임의의 Curve를 그린 후 특정한 간격과 각도, 크기 비율로 복사해 올린 후 두께를 주었다. - 슬라브 간격(층고)와 크기 비율은 GraphMapper로 조절가능하다. - 각도는 단순히 Twist 명령어를 사용한 것이 때문에 GraphMapper로 조절하는 데에는 한계가 있다. - 슬라브의 두께는 층고의 n분의 1로 설정할 수 있으며 최종본에서는 6분의 1이다. 2) 앞의 과정을 거친 후 1번에서 설명한 Core의 부피와 3번에서 설명할 Worm의 부피를 Boolean Difference하여 완성하였다.

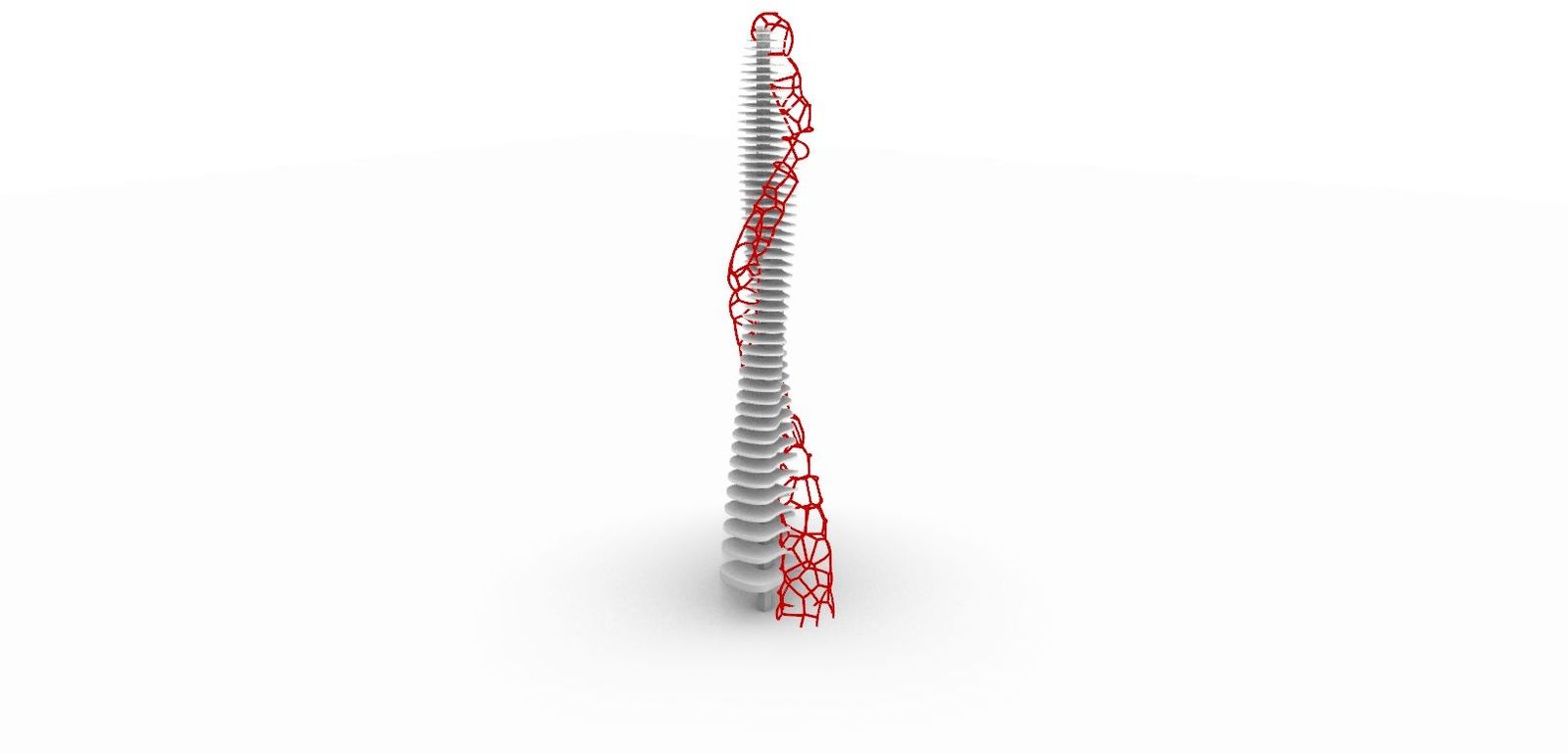
3. Worm 벽을 타고 올라가는 지렁이 형상의 구조물이다. 1) 슬라브를 만들 때 사용했던 Curve(이하 BC(Base Curve))를 층수만큼 등간격으로 분할할 수 있다. 2) 각 층 모두 BC를 변형하여 만든 것이기 때문에 BC를 등간격으로 나눈 점들은 각 층의 슬라브 경계상의 점으로 대응시킬 수 있다. 3) 1층은 첫 번째 점, 2층은 두 번째 점 ... n층은 n번째 점을 각각 추출하여 Interpolate Curve로 연결시킨다. 4) 3에서 만든 Curve를 중심으로 구간별 파이프의 두께를 부여하여 지렁이의 형상을 만든다. - GraphMapper를 활용해 구간별 두께를 변형할 수 있다. 5) Populate Geometry와 Voronoi3D를 활용해 4에서 만든 지렁이의 형상을 여러 표면으로 나누고 각 프레임을 추출하였다.

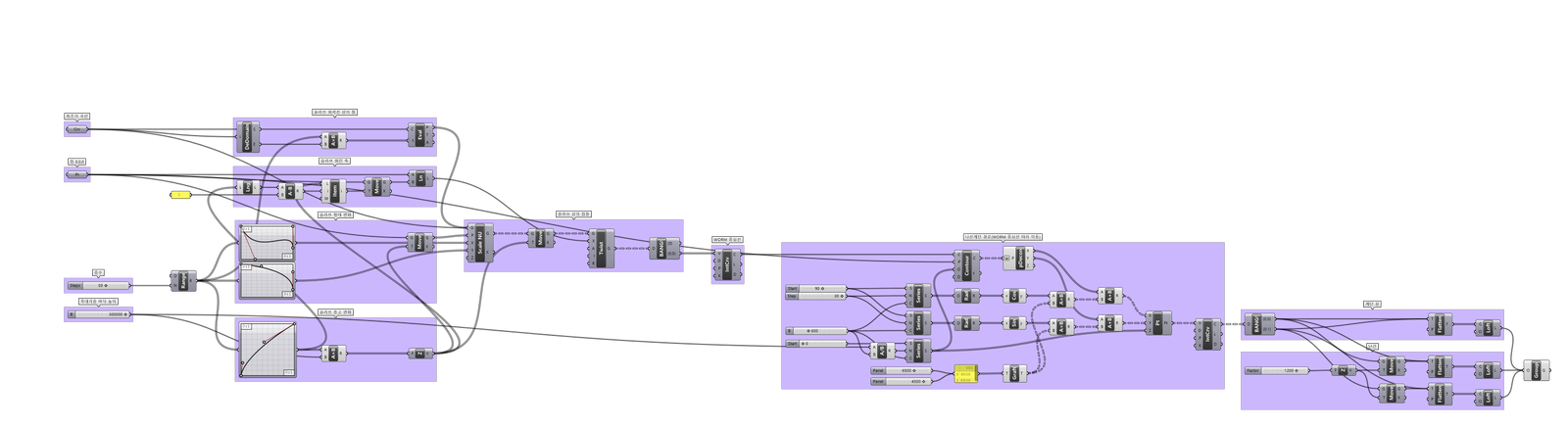
4_1. Stairs Worm 속을 지나는 나선형 계단이다. 1) 7주차에서 다루었던 스프링 만드는 알고리즘을 변형한 것이다. 2) 해당 알고리즘에서 스프링의 중심이 되는 점의 Z값을 조절하며 스프링의 형상을 만들었는데 여기에선 X, Y값 역시 바꾸었다. - 스프링의 중심이 되는 점은 Worm의 중심선이 되는 Interpolate Curve 상에 위치한다. 3) 스프링의 반경을 둘로 나누어 계단의 안쪽 면과 바깥쪽 면의 선을 따로 만들었고 이를 Loft하여 계단 및 난간을 만들었다.

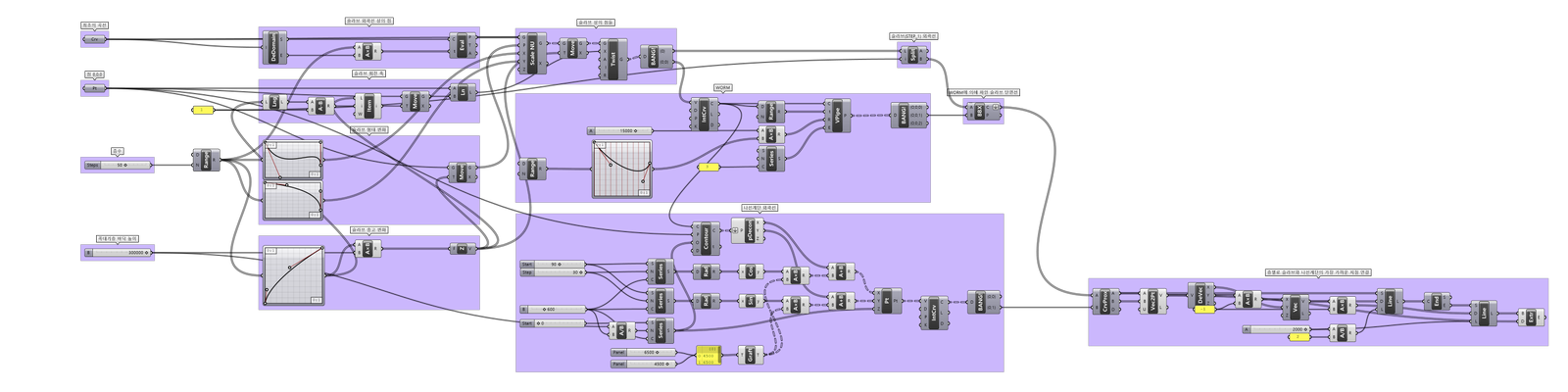
4_2. Connection Between Stairs and Slabs 사진상에서는 잘 보이진 않지만 슬라브와 나선계단을 이어주는 다리를 모델링한 것이다. 1) Curve Proximity를 이용하여 4_1에서 만든 나선계단의 바깥쪽 면(정확히는 선)과 각 슬라브 간의 최소 거리를 추출한다. 2) 1번에서 추출한 거리를 선으로 연결한 후 양쪽으로 Extrude하여 다리를 완성한다. - 이때 '양쪽'이라는 방향을 내가 직접 입력해야 했기 때문에 1번에서 추출한 거리 벡터의 X, Y 값만 추출한 후 각각 Y와 X에 넣어 벡터를 만든 후 사용했다.

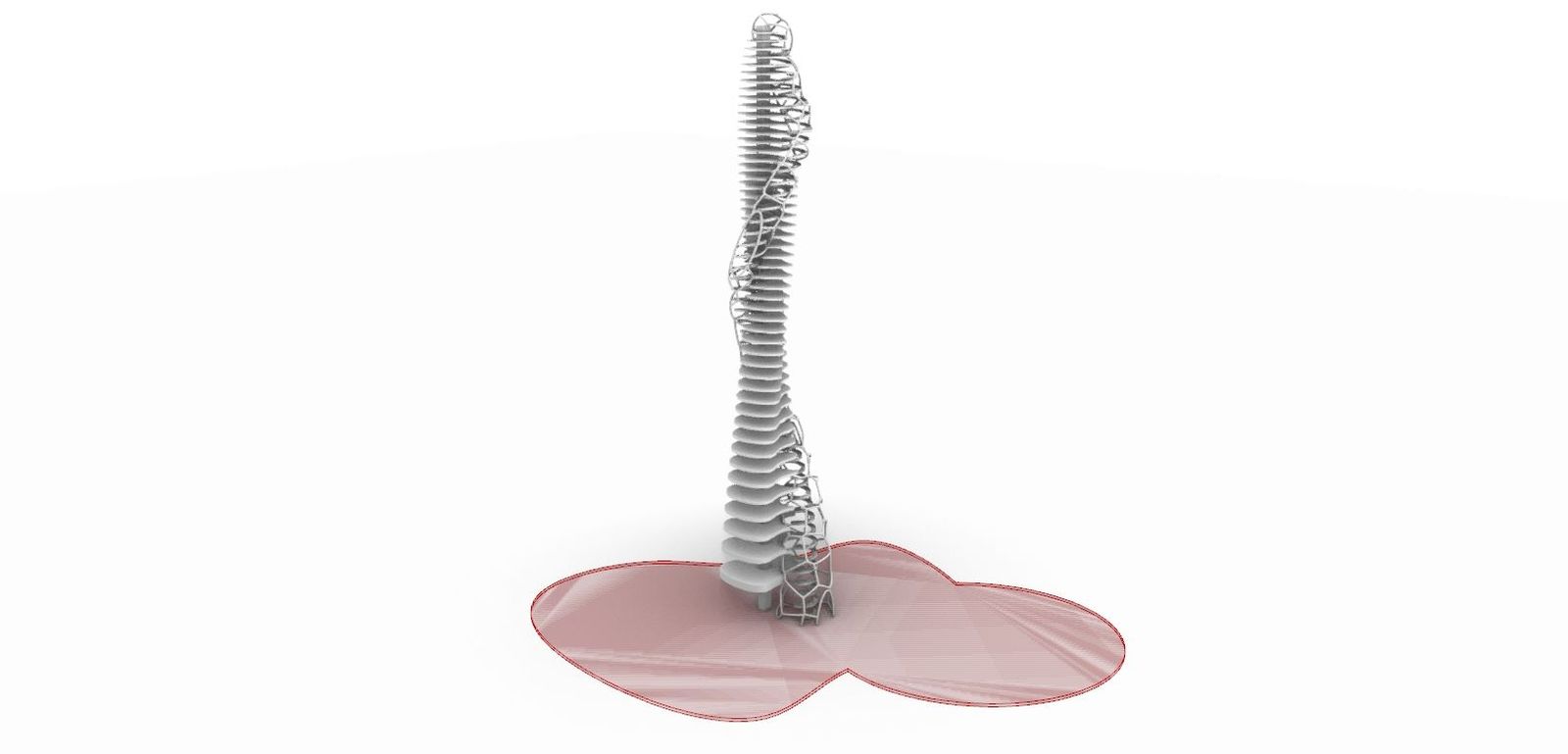
5. Base 기초가 되는 바닥 판이다. 1) 슬라브를 Loft한 것과 와 Worm이 차지하는 부피를 Boolean Union하여 전체의 매스를 추출한다. 2) Contour를 활용하여 전체 매스의 1층 바닥 높이면의 단면선을 추출한다. 3) 2번에서 구한 선을 X와 Y 방향으로 스케일을 키운 후 Extrude하여 바닥면을 완성한다.

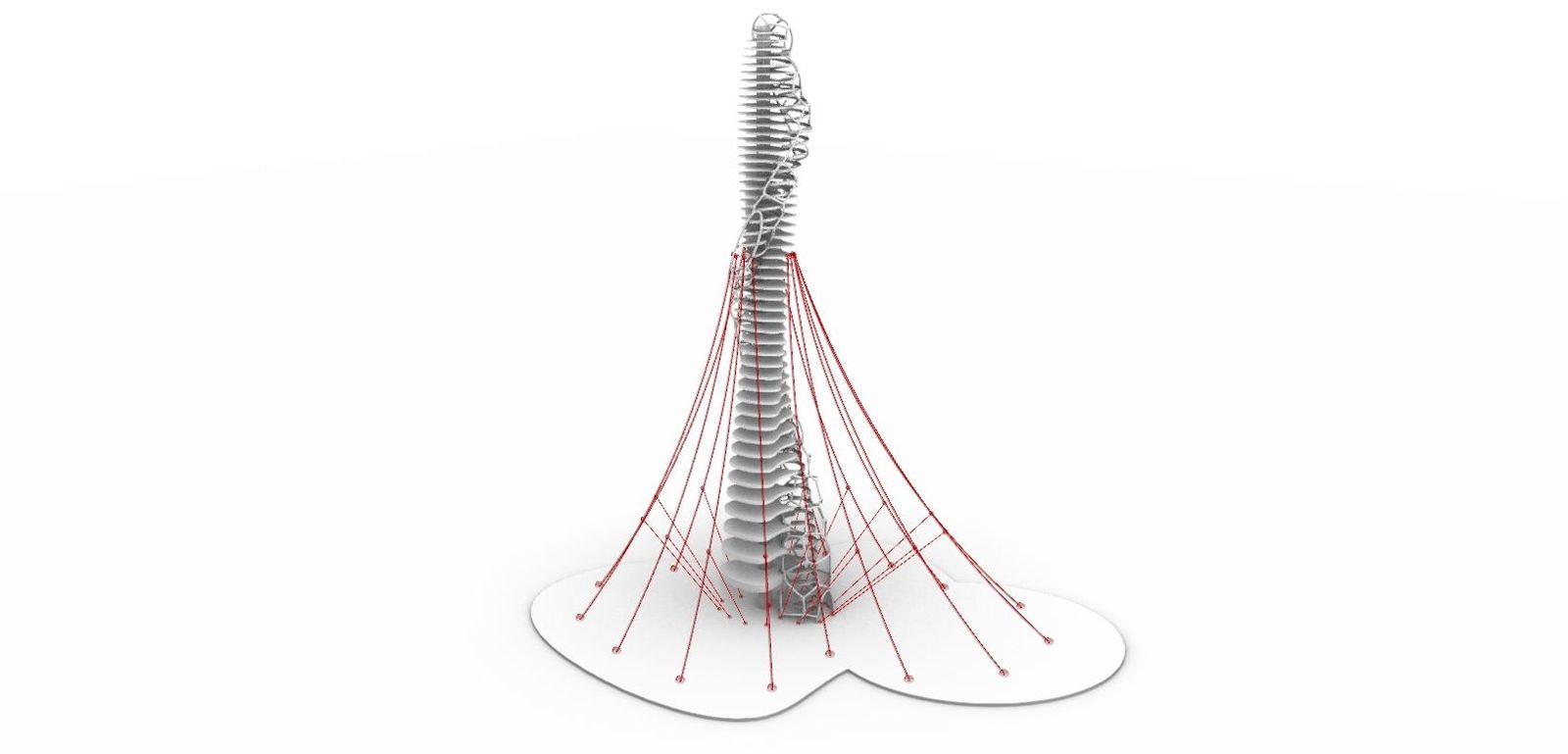
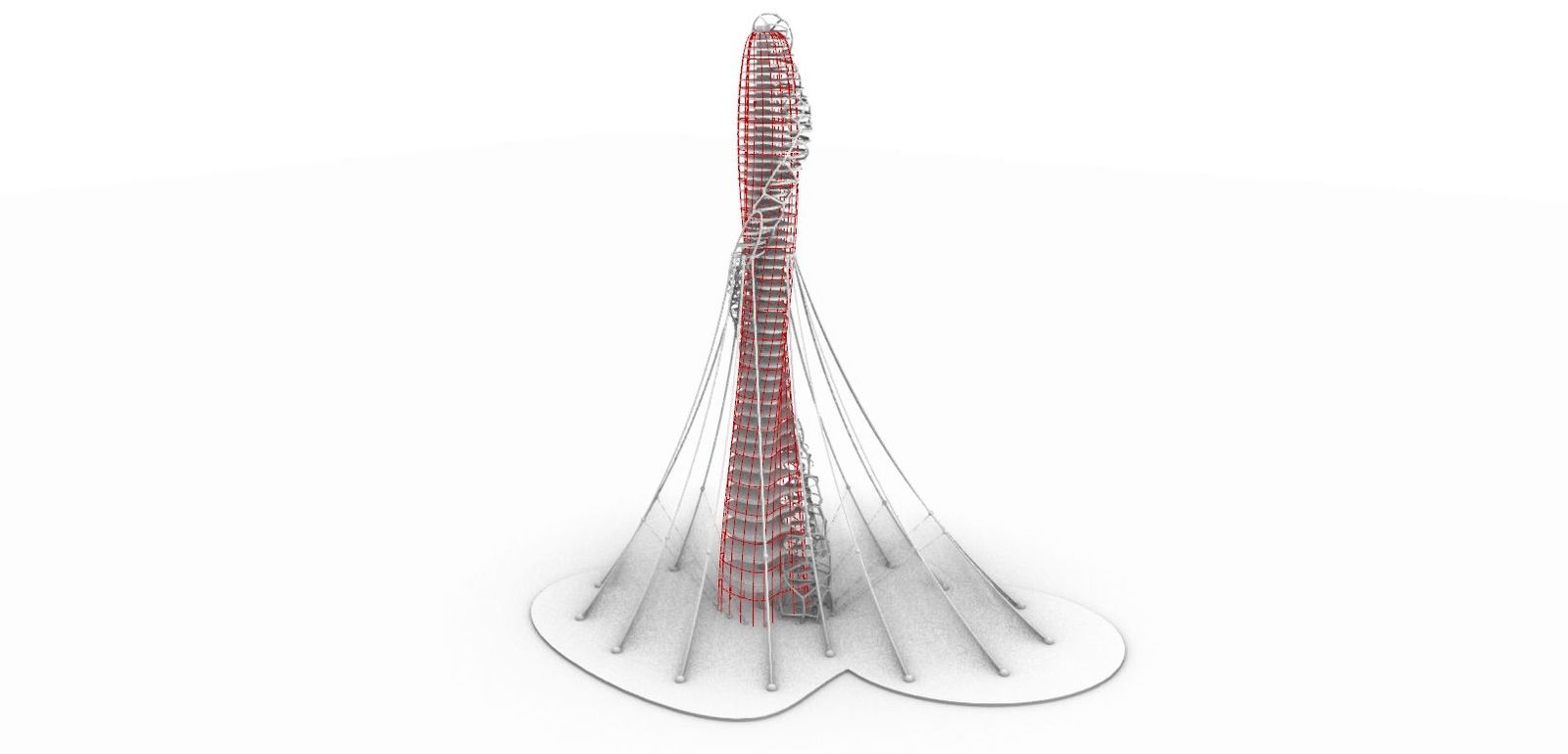
6. External Wire 타워 외부에서 지지하는 와이어이다. 1) Base를 만들 때와 동일한 방법으로 Base보다 안쪽에 선 하나를 만든 후 만들고자 하는 와이어의 수만큼 등간격으로 나누어 점들을 추출한다.(A점) 2) Contour를 이용하여 전체 매스의 n번째 층고의 단면선을 추출한다. 3) Curve Closest Point를 활용하여 1번에서 추출한 A점과 2번의 단면선의 최소거리를 구한다.(여기서 n층의 단면선 상에 찍히는 점이 B점) 4) A점과 B점을 연결한 선 상에서 전체길이 m % 상의 점을 추출한다.(C점) 5) 전체 매스의 1층 높이의 단면선과 C점의 최소거리를 구한다.(3번과 동일한 방법, 여기서 나오는 점이 D점) 6) C점과 D점을 연결한 선 상에서 전체길이 l % 상의 점을 추출한다.(E점) 7) Interpolate Curve로 A-E-B를 연결한 후 Pipe로 두께를 준다. 8) Line으로 D-E를 연결한 후 Pipe로 두께를 준다. 9) A, B, C, E 점에 각각 적절한 크기의 구를 배치하여 와이어를 연결하는 부재를 표현하였다.

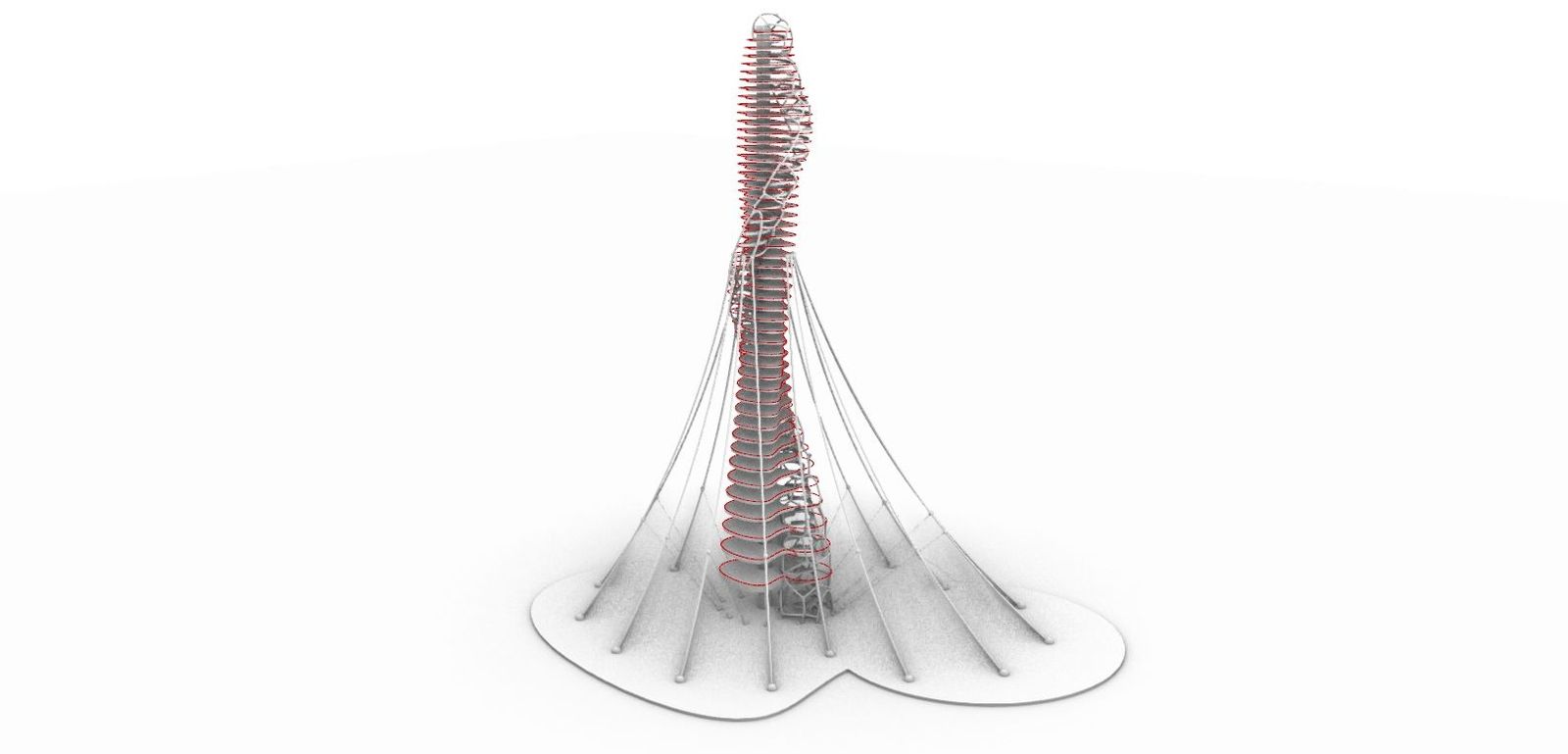
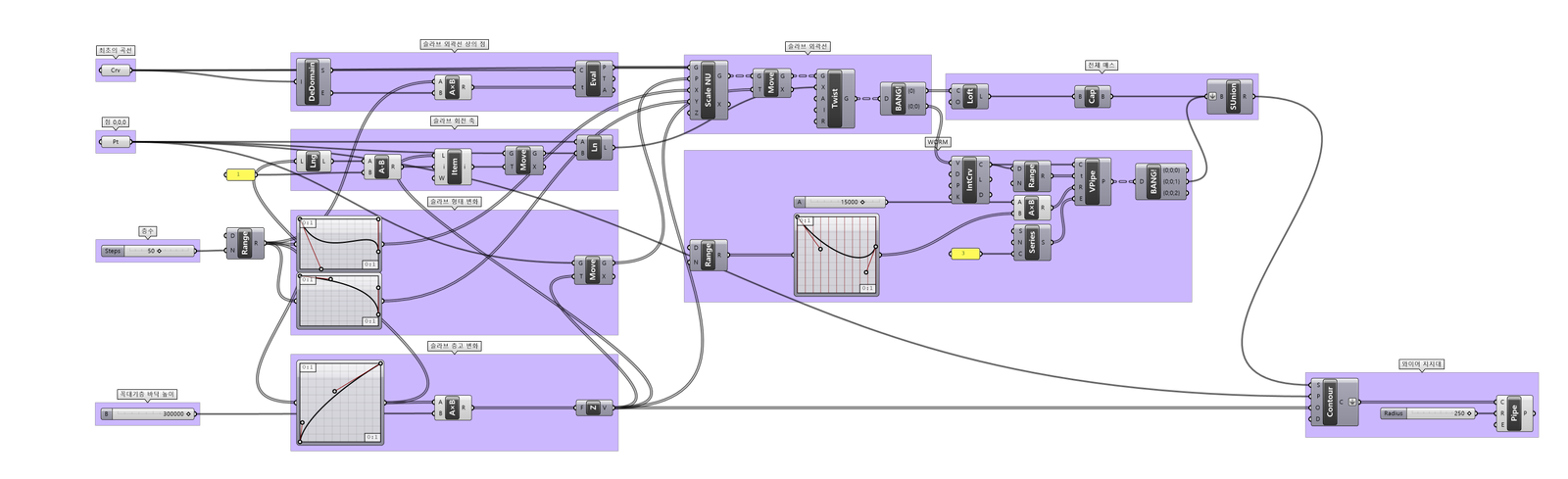
7_1. Structure for Inner Wire 타워의 파사드가 될 Hexagon Pattern(이것과 관련한 내용은 뒤에서 설명 예정)이 걸리는 와이어(Inner Wire)가 있고 그 와이어를 잡아주는 구조체가 있다. 이건 와이어를 잡아주는 구조체이다. 1) Contour를 활용하여 전체 매스를 각 층 높이로 나눈 단면선을 추출한다.(슬라브를 만들 때 사용햇던 Curve는 Worm의 형태가 반영되어있지 않아 재활용할 수 없다.) 2) Pipe를 활용하여 1번에서 구한 선에 두께를 준다.

7_2. Inner Wire (Wire for Facade) 7_1에서 만든 구조체에 걸리는 와이어이다. 이 와이어에 Hexagon Pattern 프레임이 걸린다. 1) Sub Surface를 이용하여 슬라브만을 포함하는 매스의 표면을 나눈다. 2) 1번에서 그리드로 나눈 표면들의 외곽선을 추출한 후 Pipe로 두께를 준다.

여기서 Inner Wire는 슬라브만 포함하는 매스를 기반으로, 7_1의 Structure는 전체 매스를 기반으로 만든 이유를 간단하게 설명하자면 1) 7_1의 Structure는 Inner Wire 뿐만 아니라 Worm 역시 잡아주는 역할을 하는 것으로 상상하였다. - n층 높이에서 External Wire를 잡아주는 구조체 역시 7_1의 Structure이다. 2) 7_1의 Structure가 Worm내부의 나선계단과 겹치기 않기를 바랬다. 3) Inner Wire가 지탱하는 Hexagon Pattern은 Worm의 표면상에는 존재하지 않기 때문에 Inner Wire가 전체 매스를 기반으로 만들어질 필요가 없다.

7_3. Hexagon Pattern 파사드 상에 존재하는 육각형 모양의 패턴이다. 1) Surface Box를 이용하여 7_2에서 만든 그리드에 모듈을을 배치한 후 Worm이 차지하는 매스만큼 Boolean Difference하여 제거한 후 남는 모듈을 Boolean Union하여 하나의 Polysurface로 만든다. - 모듈의 형태는 아래 PPT에서 설명 - 원래는 Boolean Unoin 후 Boolean Difference를 하는 것이 더욱 간편하지만 그래스호퍼 모델링 계산 상의 오류로 Boolean Unoin을 하면 Non-Manifold Polysurface가 되어 Boolean Difference를 할 수가 없었다.

아래에서 위를 올려다본 뷰이다.

Worm 안을 지나가는 나선계단과 표면의 육각형 그리드가 잘 보이는 뷰이다.

최종 제출 PPT이다. Variation과 관련한 내용이 추가되었으며 계단과 관련한 두 단계, 그리고 기초와 지지 와이어는 서로 연관된다고 생각되어 하나의 슬라이드에 넣기 위해 PPT상에서의 순서는 디자인 프로세스의 순서와 일치하지는 않는다.