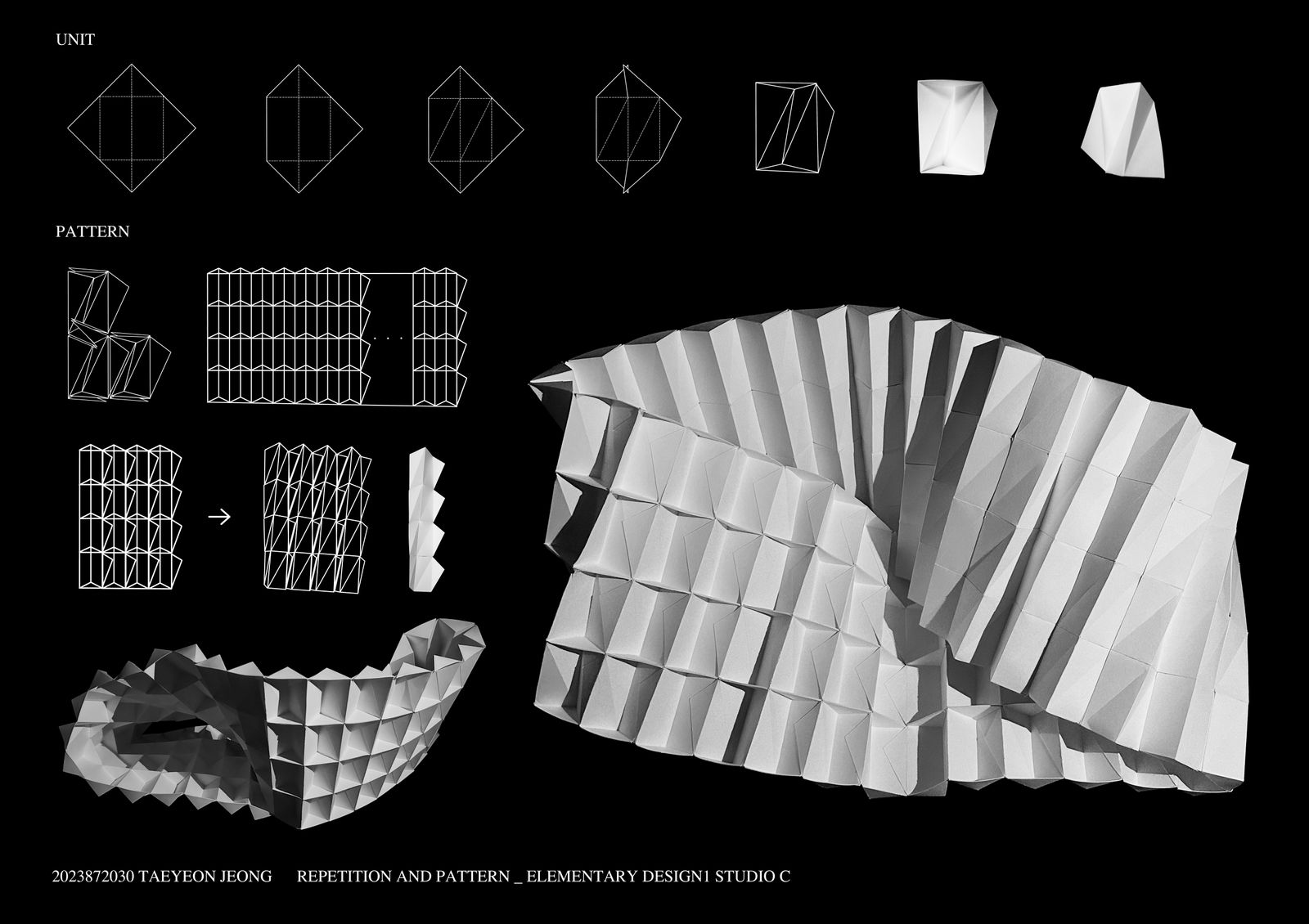
자연에서 반복과 패턴을 찾고자 했다. 기둥을 타고 계속해서 올라가는 포도나무를 보고 영감을 받았다. 사각기둥을 비틀어서 나선형을 구현하고자 했다. 사각기둥은 두 개의 삼각기둥을 이어 붙여 만든다. 90x90 정사각형 켄트지를 대각선 방향으로 놓고 각 변의 중심에 내접하는 작은 정사각형을 만든다. 작은 사각형은 세로로 길게 나뉘어 삼각기둥의 옆면이 된다. 비틀어진 사각기둥을 만들기 위해 기둥 옆면을 각각 대각선으로 접어준다. 위아래 나머지 삼각형 부분은 기둥의 밑면이자 수직 방향으로 단위체를 이어 붙일 때 날개로서 기능할 수 있도록 기둥 면의 경계에 따라 절반으로 자른다. 양옆 나머지 삼각형은 수평 방향으로 단위체를 이어 붙일 때 날개로서 기능할 수 있도록 기둥의 대각선과 평행하게 자른다. (나중에 한쪽 방향으로 이어 붙이면서 옆 날개는 한 개로 충분해서 왼쪽 날개를 제거했다.) 이등변직각삼각형을 밑면으로 한 삼각기둥을 단위체로 결정했다.

삼각기둥을 두 개 이어붙여 사각기둥을 만드니 수직으로 이어붙이는 것 이상의 결합을 기대하기 어려웠다. 수평으로 단위체를 결합할 때 사각기둥으로 한정하지 않고 두 개가 아닌 세, 네 개, 그 이상을 이어 붙이다 띠 형태를 만들게 되었다. 최종적으로 수직으로 4개, 수평으로 28개를 이어붙여 112개를 이용한 넓은 띠 형태를 완성하였다.

사각기둥을 비틀기 위해 대각선으로 접었던 기둥 옆면의 선이 전체 띠를 곡선으로 휘어지게 하여다. 곡선 띠의 특징을 살림과 동시에 단위체의 앞, 뒷면을 한 번에 보여줄 수 있는 ‘뫼비우스의 띠’를 최종 모형으로 결정했다.