정사각형 큐브라는 기본 단위체를 변형하는 과정에서 '직각에 반하는 요소'를 탐구하였고, 그 결과 '사선'을 최종 방향성으로 잡았다.
정사각형 큐브 중심부를 '사선으로 1번 자른 단위체'와 '위 아래 사선으로 2번 자른 단위체'를 두고 고민함. (각 이미지1, 이미지2)
이번 과제의 핵심 요소가 '공간'인 만큼 공간을 더 잘 나타낼 수 있는 1번 이미지의 단위체를 최종으로 결정함.
또한, 매스 단계의 크리틱 중 2번 이미지의 단위체에서의 '동선의 순환'이라는 아이디어가 나왔기에 이를 1번 이미지의 단위체에 녹여보고자 함.
모형의 메인 이미지에서 가장 두드러져 보이는 것은 '사선'과 '계단'이다. 사선이라는 요소를 더욱 극대화 할 수 있는 방안을 모색하였고, 그 결과 '계단'을 활용하고자 하였다.
단위체에서 사선의 각도를 정하는 과정에서 여러움이 존재했다. 기존 매스 모형에서 사선을 40~45도 각도로 설정하였을 때 전체적인 비례감을 느낄 수 있었다. 하지만, 현실적으로 40~45도 각도의 계단은 사용자가 불편함을 겪는 각도이다. 아무리 훌륭한 구조와 형태를 지닌 건축물이라도 건물을 사용하는 이용자가 불편함을 겪어서는 안된다고 생각하였다. 따라서 계단의 각도는 약 33도, 가로 30cm, 세로 20cm, 폭 120cm로 정하였고, 이 수치는 우리가 평소 많이 사용하면서 불편함을 겪지 않는 계단의 사례인 건축공학관에서 비롯된 수치이다.
사선의 각도를 수정 후 33도로 설정하여 처음 스터디 해봤을 때는 건물의 전체적인 비례감을 느끼지 못했지만, 수 많은 모델링과 수정을 통해 약 33도 각도에서도 비례감을 찾을 수 있었다. 단위체의 전체 높이를 낮추고, 우측으로 확장시킴.
모형의 3층에 보이는 떠있는 사선 부분에 대한 고민이 이루어졌다. 이 부분을 '평평한 면 또는 계단'을 설치하여 '바닥이 있는 공간'으로 활용할 수 있었다. 하지만, 이렇게 방향성을 잡는다면 건물의 구조상 우측으로 하중이 더 많이 쏠려 안정성에 대한 우려가 존재한다. 또한, 건물의 주요한 특성인 '사선'을 더욱 부각시키는 것이 아니라 죽이는 요소라고 생각하였다.
따라서, '캔틸레버(cantilever)' 구조의 개념을 적용함으로써 구조적 안전성을 고려하고 건물의 주요한 특성 또한 살리고자 하였다.
앞서 언급했던 '동선의 순환'이라는 요소를 위의 이미지에서 확인할 수 있다. 1층에서 2층으로 올라가면 좌측, 우측(외부 문), 정면 공간으로 동선이 이어짐. 2층에서는 외부 또는 내부를 통해 3층에 올라갈 수 있음. 내부에서 3층으로 올라갔다면, 외부 계단을 통해 2층으로 내려오거나 3층으로 올라갈 수 있음. 외부에서 3층으로 올라갔다면, 내부 계단을 통해 2층으로 내려올 수 있음.
따라서, 동선이 순환됨을 확인할 수 있다.
3층에서 4층으로 올라가는 이용자의 시점이다.
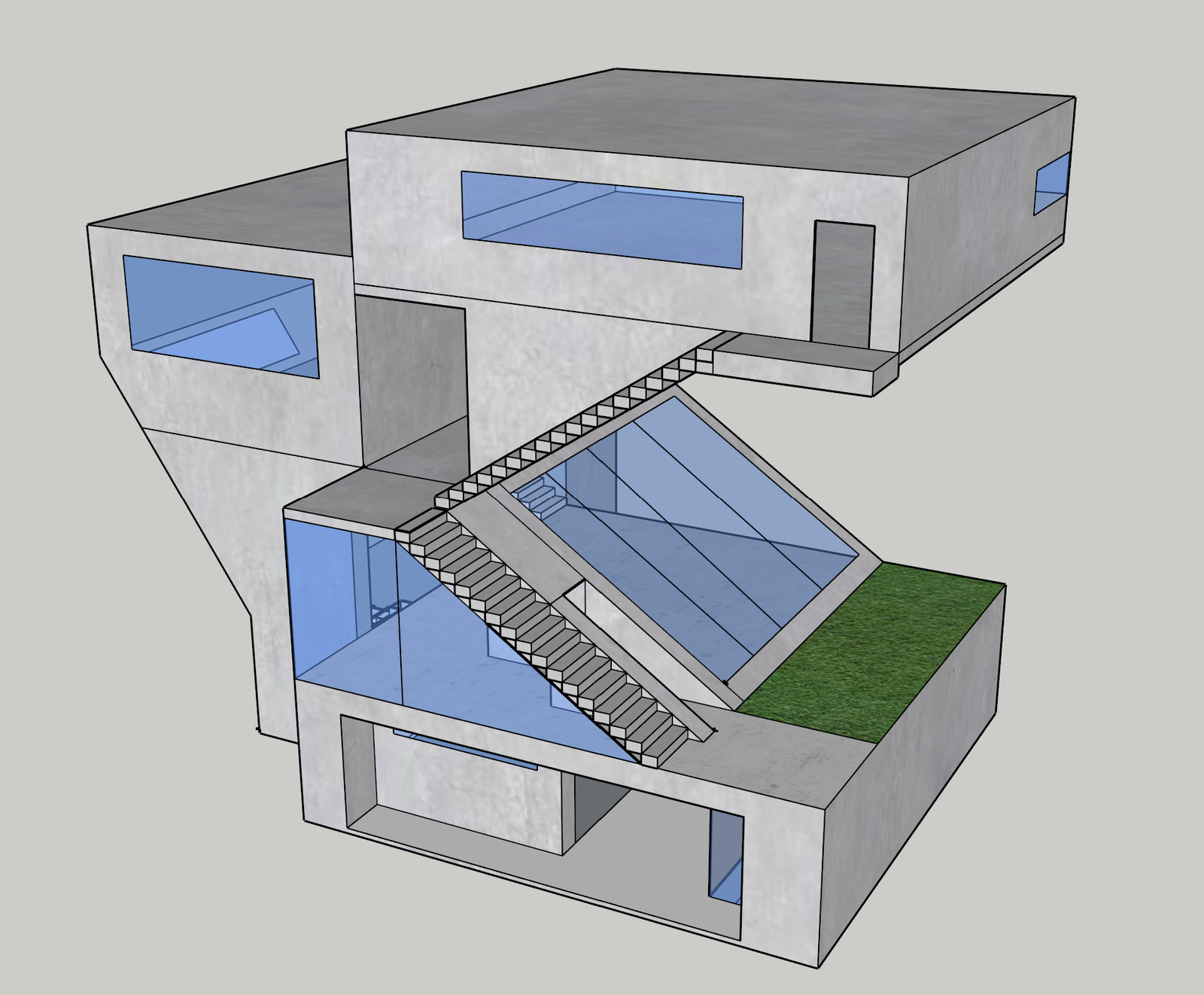
스케치업 프로그램을 활용하여 모델링 작업을 진행하였다.
아래는 1층, 2층, 3층, 4층 평면도와 단면도, 그리고 입면도와 엑소노메트릭(axonometric)이다.
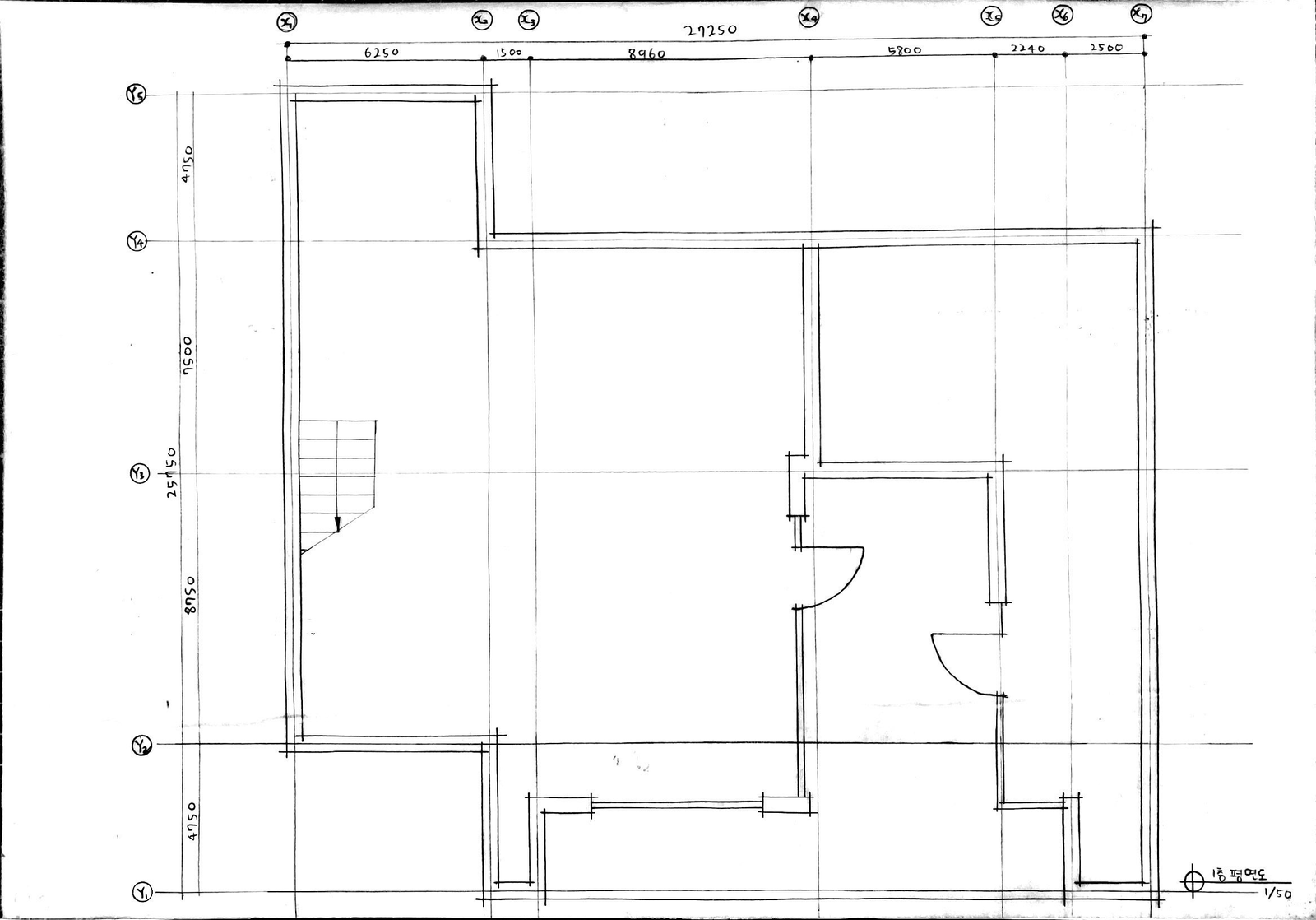
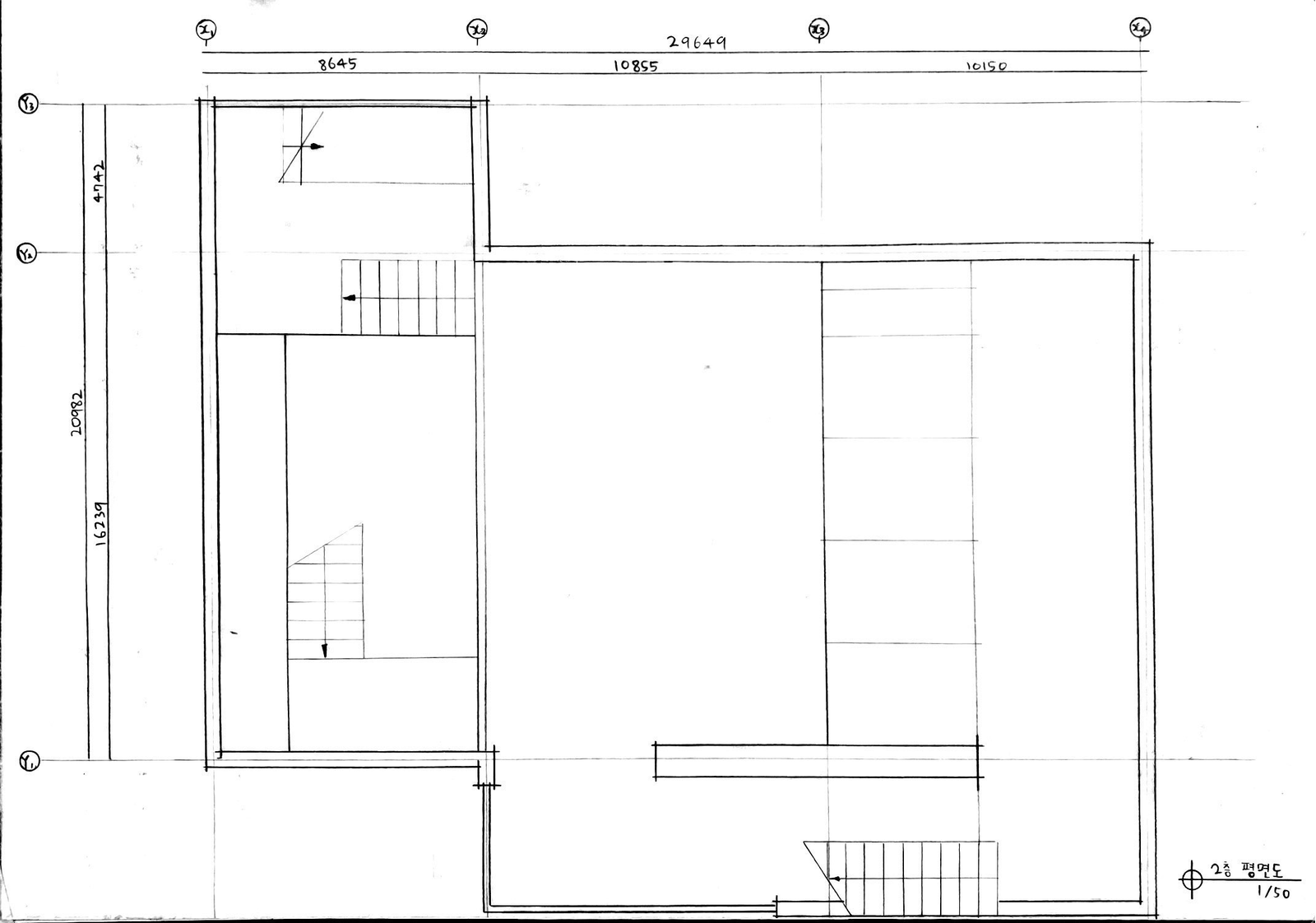
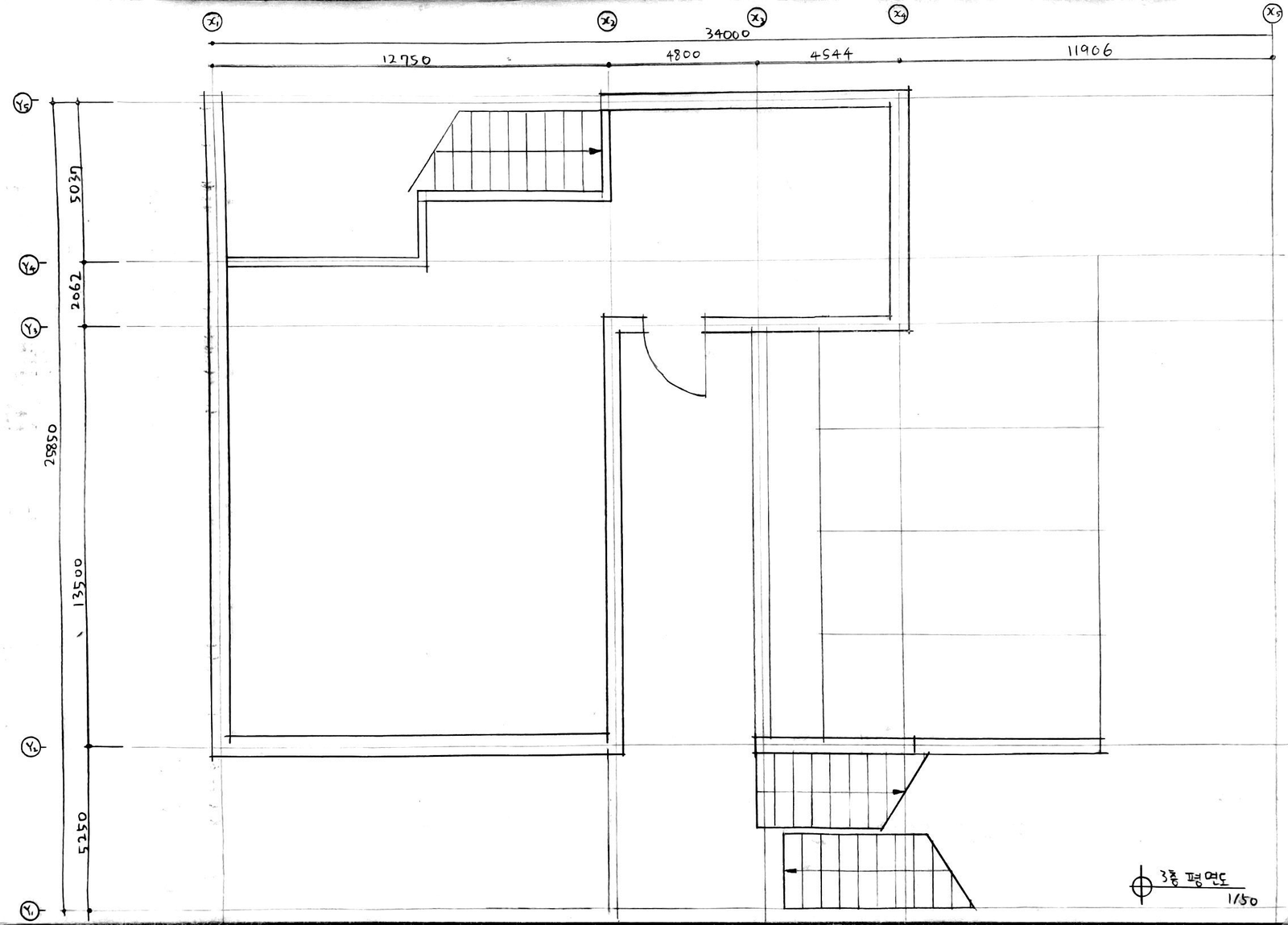
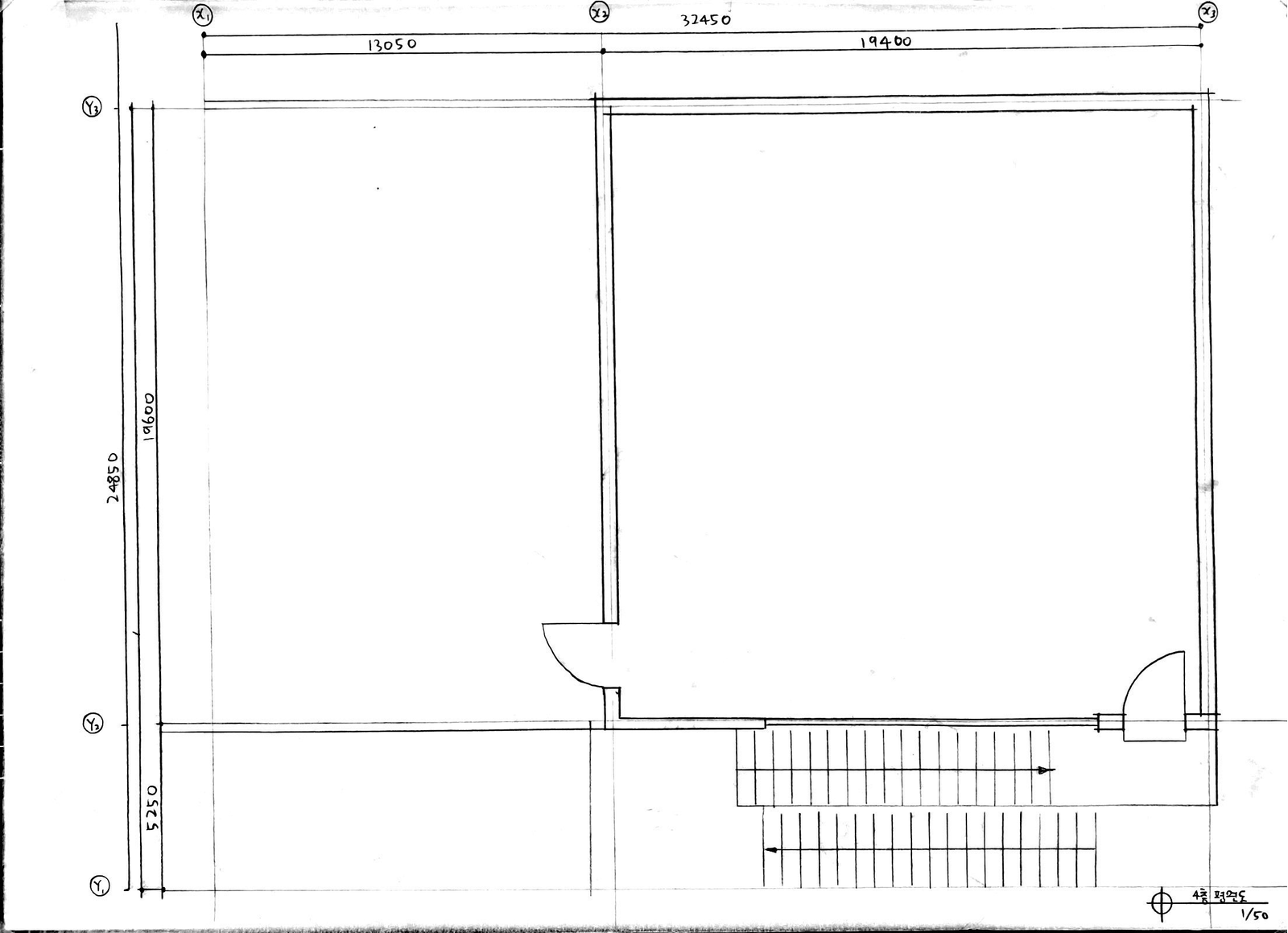
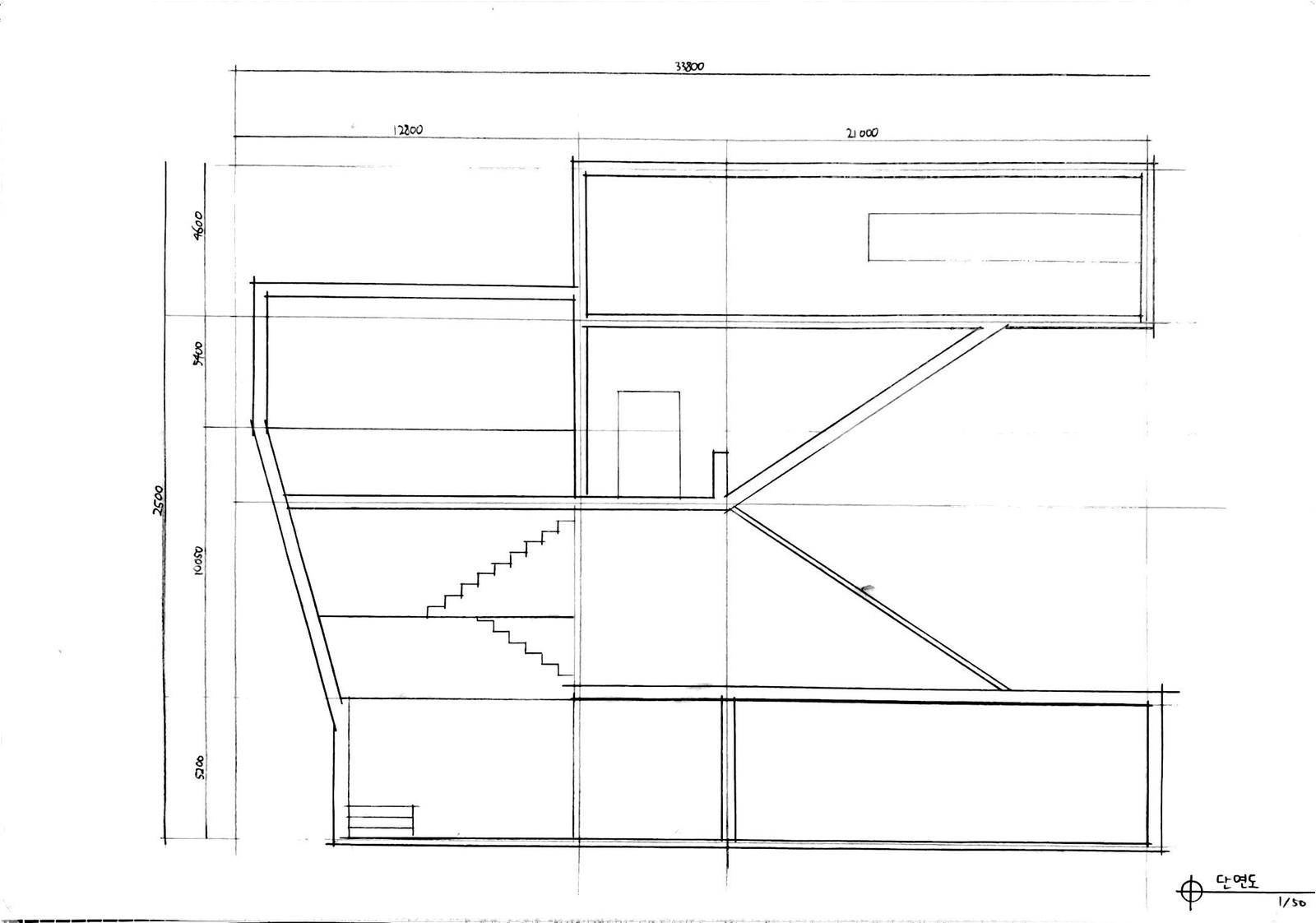
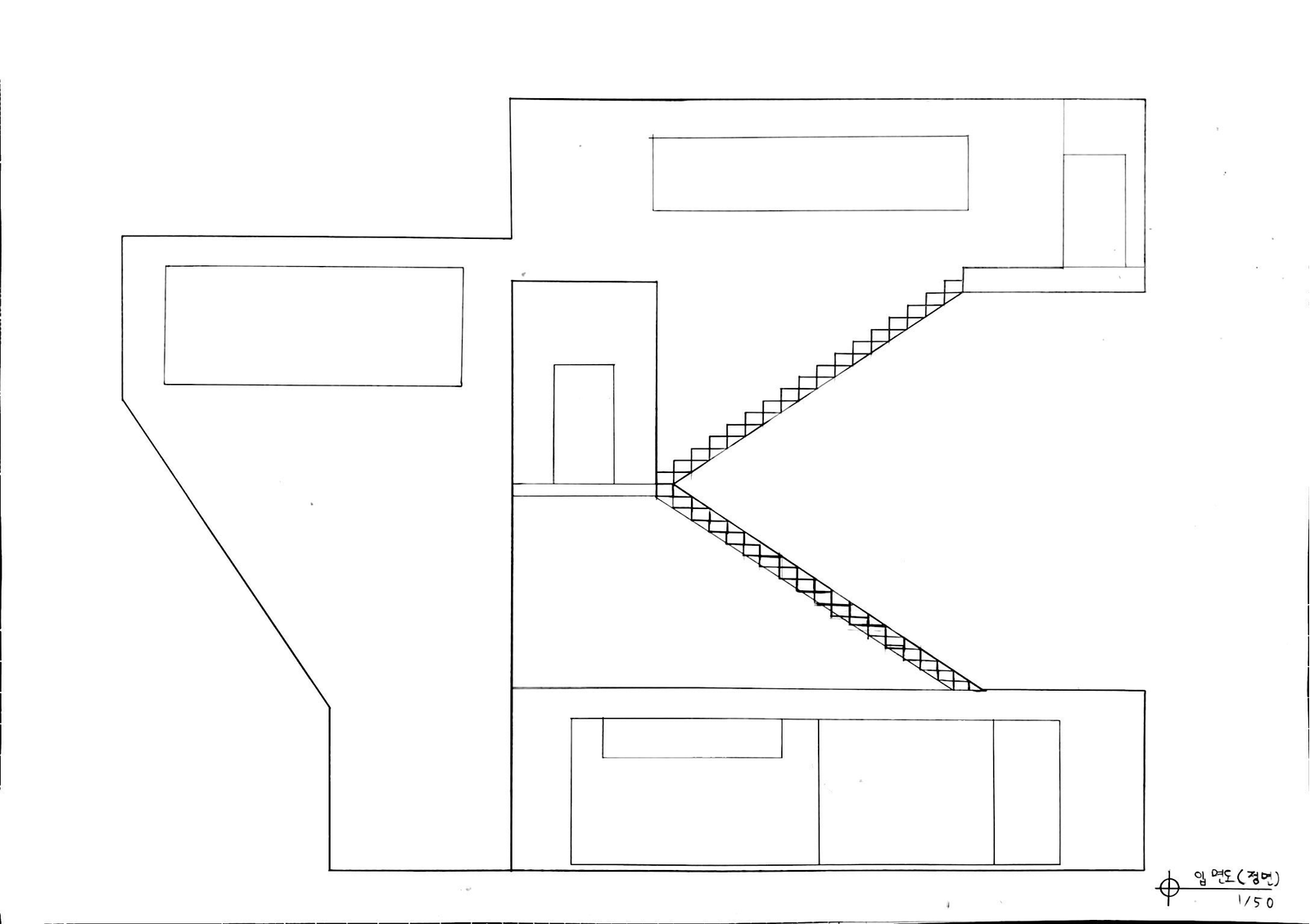
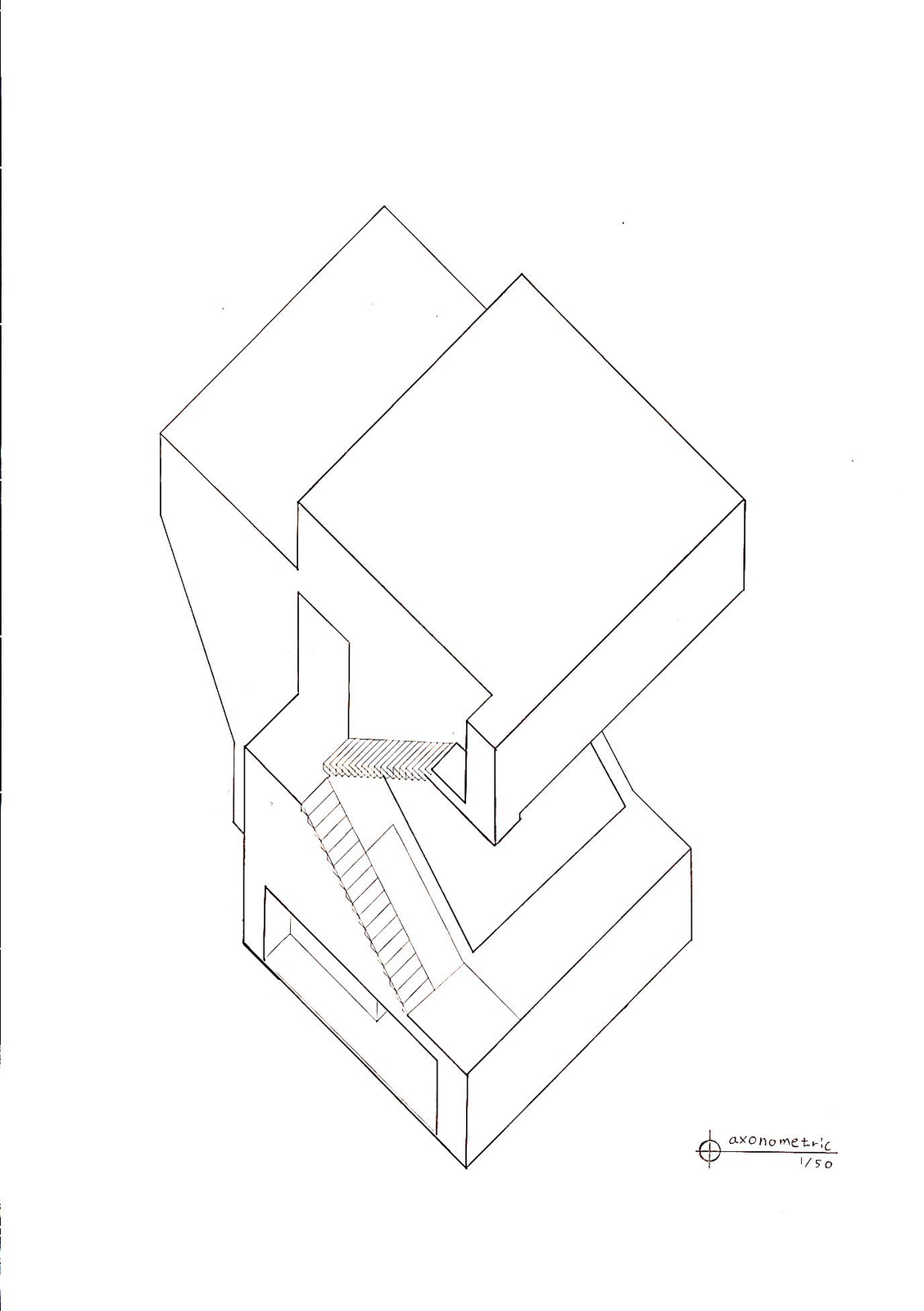
Copyright © uosarch.ac.kr., Some rights reserved.