3D TESSELLATION Doojin's Cube _ 동일한 개체를 반복하여 공간을 꽉 채울 수 있을까? 큐브 생성 원리는 정육면체의 기본 큐브에서 x축, y축, z축으로 첨삭 도형을 더하고 빼는 것이다.

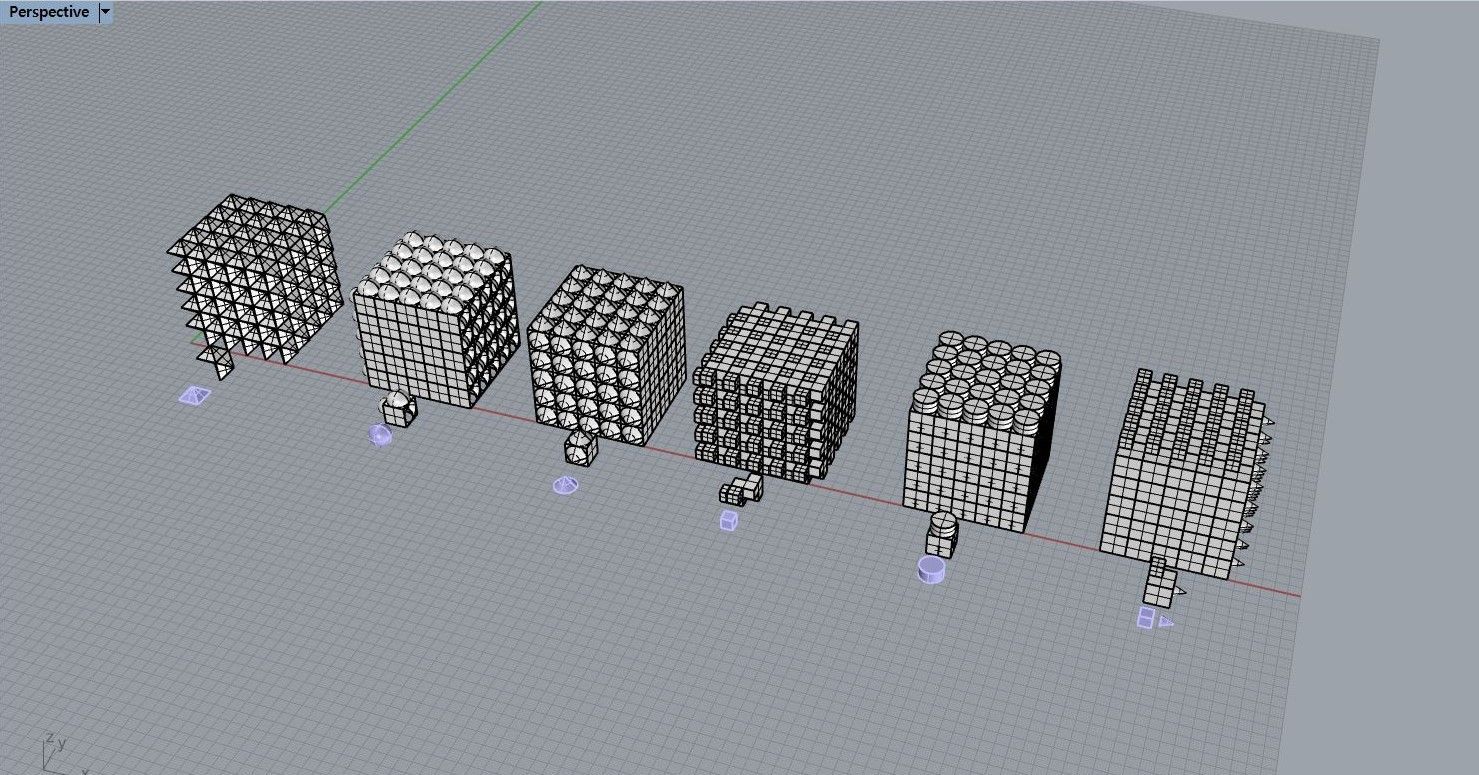
이 원리를 바탕으로 Doojin’s cube의 기본 모듈을 포함한 총 여섯가지의 3d tessellation 모듈을 생성했다.

첫 번째 모델과 네 번째 모델을 종이를 이용해 만들어 본 페이퍼 크라프트 모델이다.

스터디 모델 중에 Doojin's cube에 부합하지 않는 큐브들이 있고 비교적 형태와 원리가 단순하다고 생각해 정육면체에 원기둥의 절반을 더하고 빼는 과정을 통해 새로운 큐브를 만들었다.

처음 이 큐브를 제작할 때는 반지름이 5인 원기둥을 이용해 정육면체에 딱 맞게 더하고 빼려 했으나 doojin's cube에 부합하지 않음을 알게 되었다. 시행착오 끝에 반지름이 2.5인 원기둥의 절반을 이용해 정육면체 각 6면의 중간에서 boolean difference와 boolean union하여 큐브를 제작했다.

새로운 큐브를 크라프트지로 제작한 페이퍼 크라프트 모델이다.

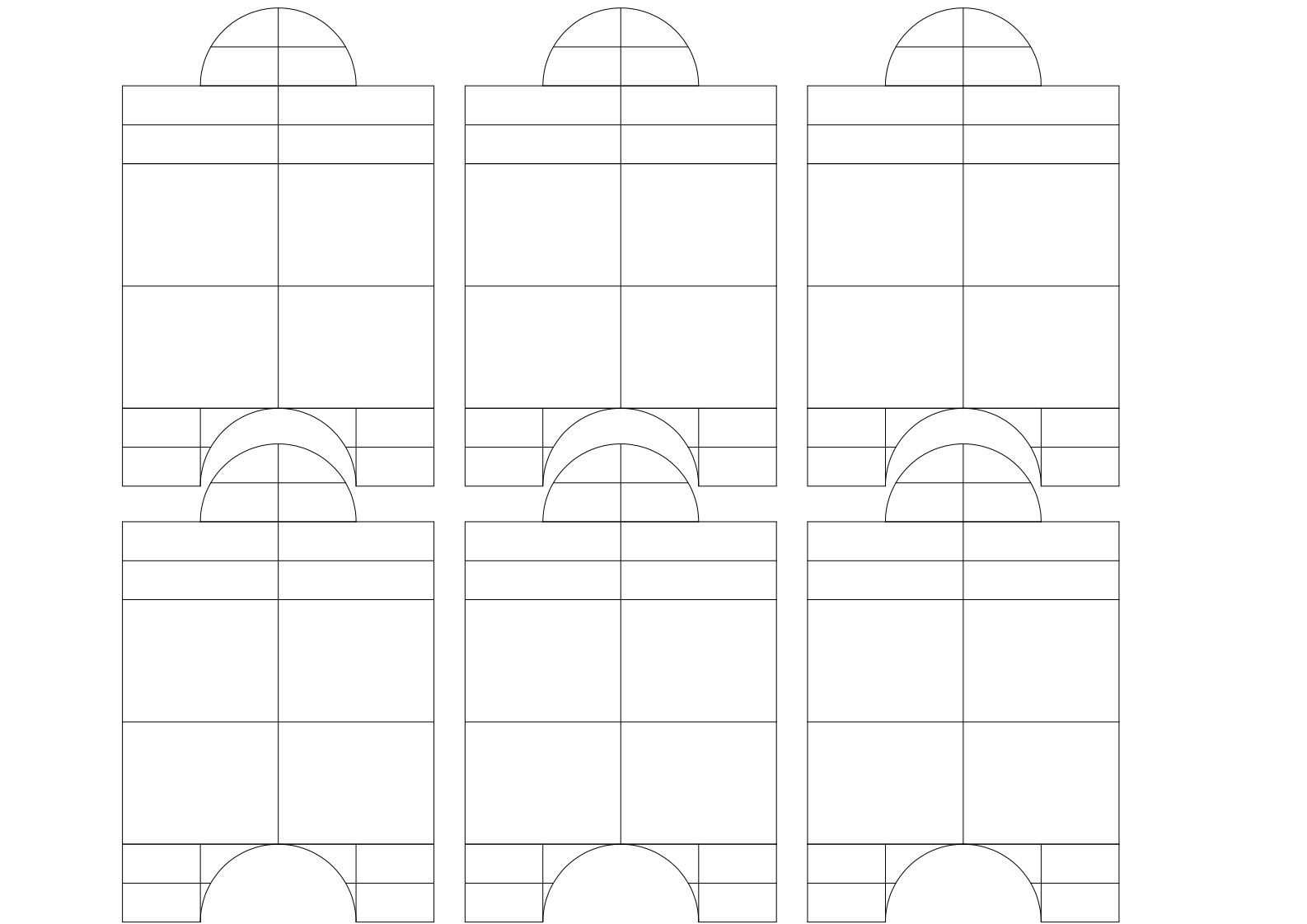
모델을 만들 때 이용했던 전개도이다. unrollsrf를 사용해 만든 전개도는 여러 부분이 겹쳐 정확한 모델을 만들기 어려웠다. 따라서 최대한 간소하게 여섯 면을 따로 분리하여 만들기로 하였다. 넓은 직사각형 부분을 세 개는 볼록하게, 세 개는 오목하게 하여 이어 붙이는 방법으로 페이퍼 크라프트 모델을 제작했다.

3D 프린터로 제작한 모델의 모습이다.

큐브를 실물로 결합하다보니 새로운 결합 방식을 찾을 수 있게 되었다. 첫 번째 사진은 큐브를 같은 방향으로 결합한 모습이다. 두 번째 사진은 큐브를 x축,y축,z축으로 각각 180도 회전해 결합할 수 있음을 보여주는 결합 방식이다.

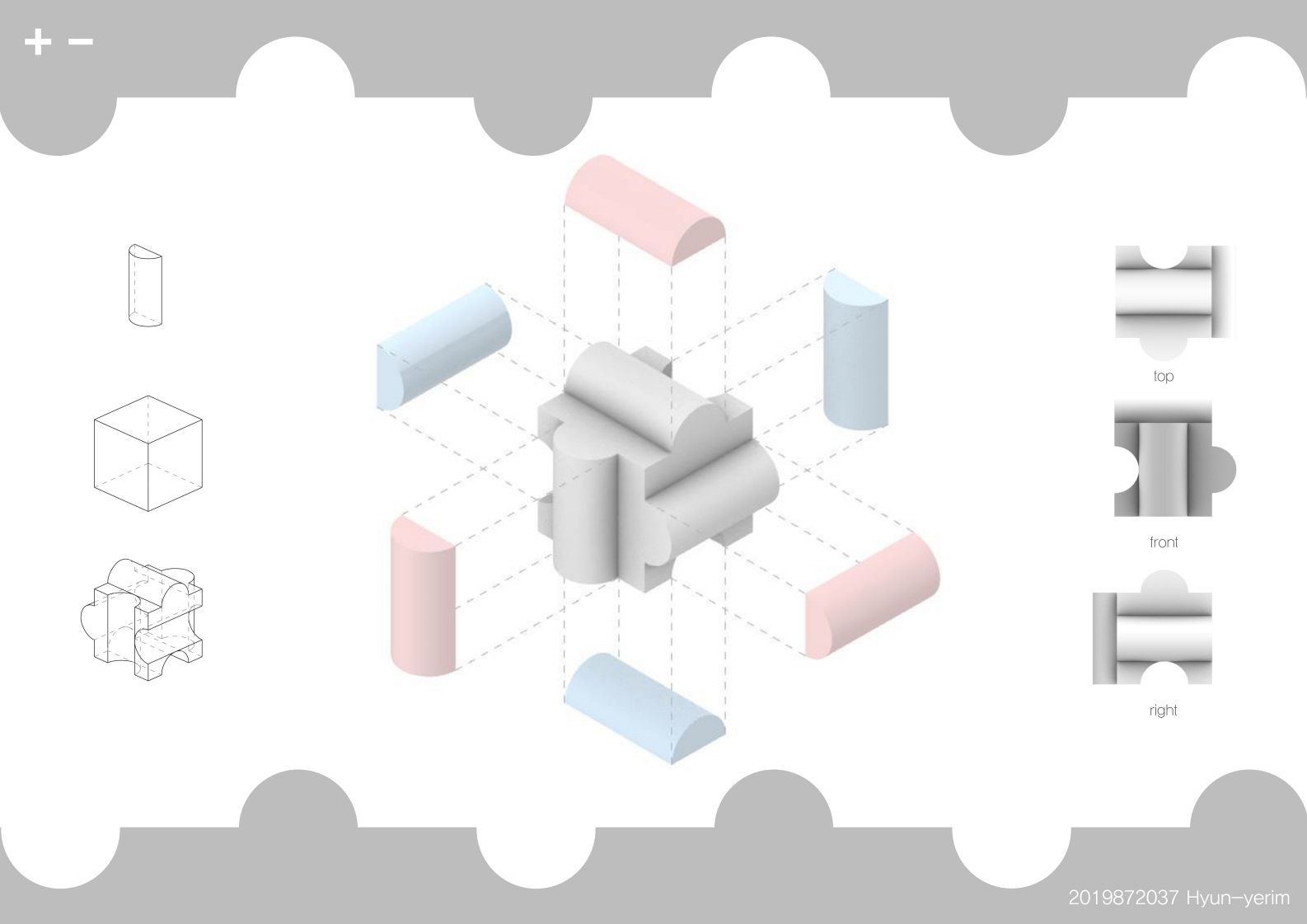
다이어그램 패널이다. 모델의 구성원리와 사방에서 바라본 큐브의 결합모습을 확인할 수 있다.

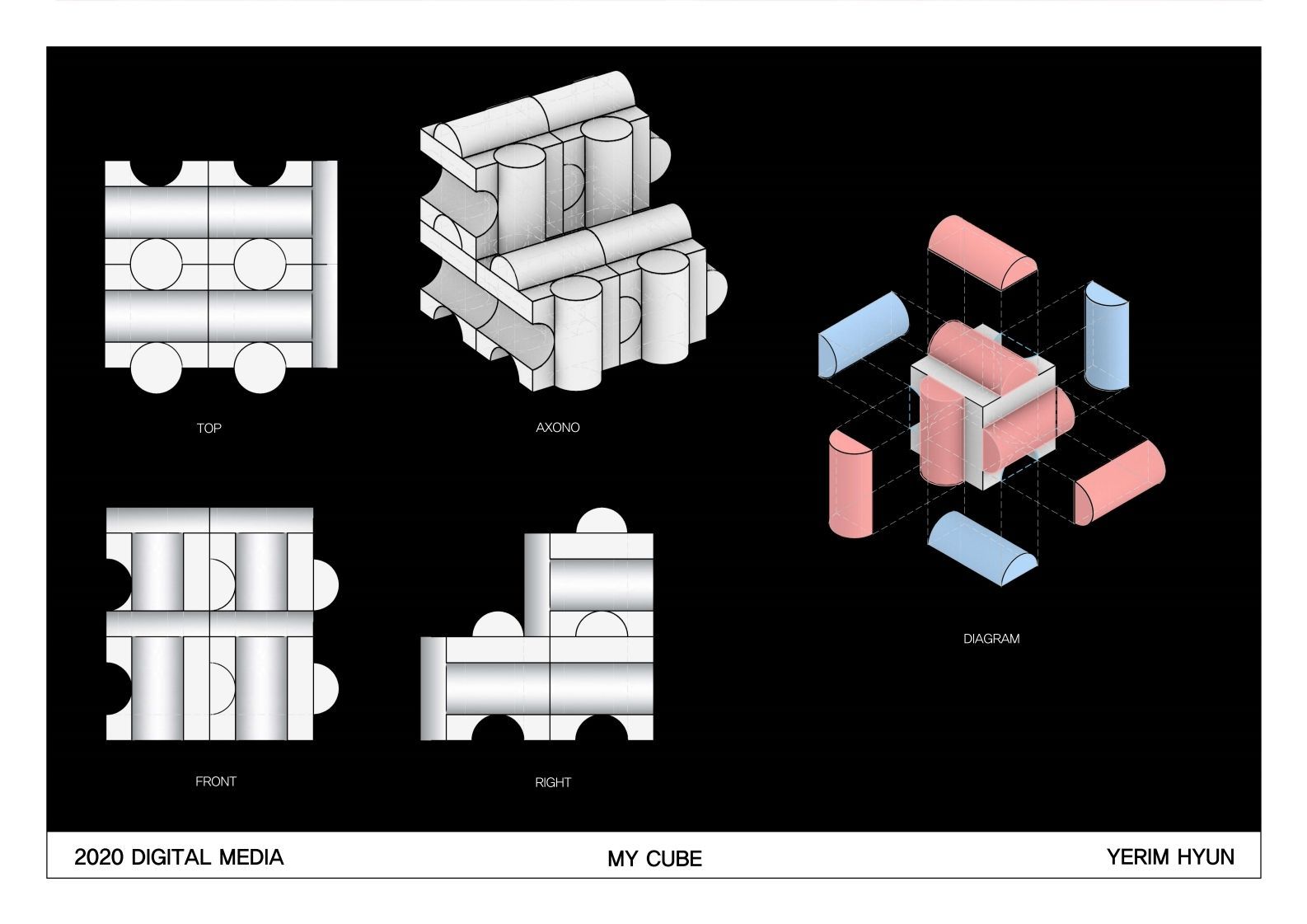
최종 패널이다. 하나의 큐브 자체에 초점을 맞추어 만든 첫 번째 패널이다. 큐브의 구성 원리와 하나의 큐브를 위, 앞, 오른쪽에서 본 모습을 나타내었다. 테두리에는 큐브 하나가 가진 패턴을 넣어 이를 강조하였다.

큐브 간의 결합방식에 주목한 두 번째 패널이다. 큐브를 결합하는 방식에 따라 서로 다른 패턴의 결합체를 확인할 수 있다. 또한 하나의 큐브로 전체 공간을 채울 수 있음을 보여주기 위해 결합체의 개수를 늘려가는 모습을 크게 배치하였다.

패널 간의 통일성이 부족하다는 피드백을 듣고 첫 번째 패널의 패턴을 이용하여 수정한 두 번째 패널의 최종 모습이다. 위 결합체의 패턴은 오목이나 볼록이 한 면에 똑같이 반복되는 반면 아래 결합체의 패턴은 오목과 볼록이 교차하며 반복됨을 강조하기 위해 테두리에 각 규칙에 맞는 패턴을 넣었다.