(위 사진에서 왼쪽은 1차 과제에서 사용한 단위모듈3이며 오른쪽은 단위모듈3을 3개 중합한 파빌리온 단위모듈이다.) 1차 과제의 모듈을 이용하여 파빌리온을 만드는 것이 이번 과제였다. 나의 1차 과제에는 단위체가 모여서 또 다른 단위체를 이루었고 그 과정이 반복되기 때문에, 여러 종류의 단위체가 있는데 그 중에서 특별히 3번째 단위체를 선택하여 최종 파빌리온을 제작하였다. 1차 과제에서 나타난 나의 최종 완성 모형의 특징을 잘 나타낼 수 있다고 생각했기 때문이다. 단위모듈3이 3개 모여서 파빌리온의 한 단위체를 만든다. (1차 과제 때 모형에서는 단위체3을 4개 중합하여 단위체4를 만들었다. 하지만 단위체3을 여러 개 중합할수록 그 높이가 낮아지고 너비가 길어지기 때문에, 이번 과제에서는 단위체3을 3개 중합시켜 높이감을 보다 더 느낄 수 있게 하였다.) 이번 과제에서는 우드락으로 파빌리온을 제작하였는데, 1mm우드락을 사용하였다. 또한 만드는 과정에서 단위체를 조금 단순화 시켰기 때문에 일부 삭제된 부분도 있다.

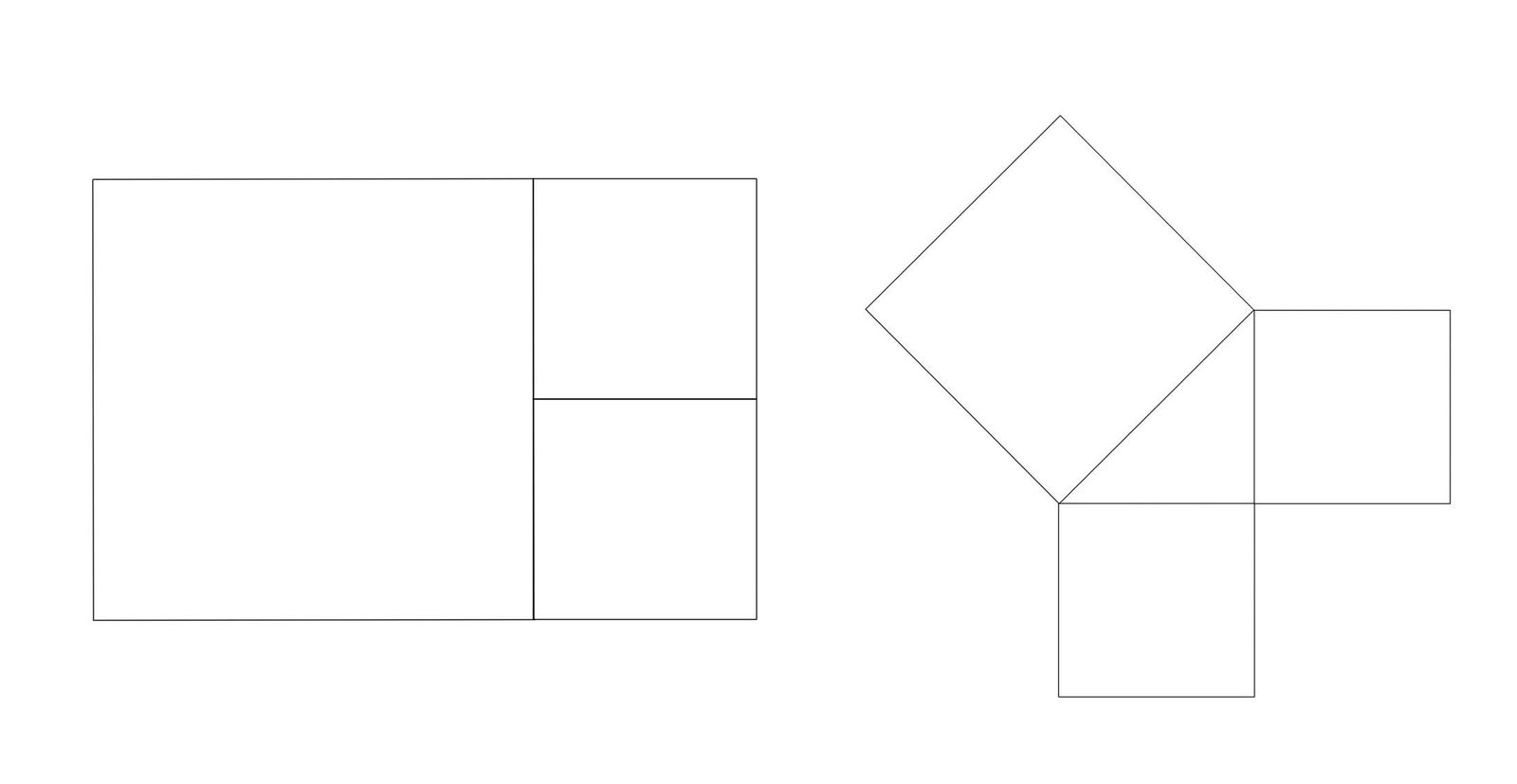
이번 파빌리온을 만들 때, 파빌리온에 사용할 한 단위체를 어떻게 배열할지 고민하다가 수학적인 개념을 사용하였다. (단위체를 정사각형으로 단순화시켜서 생각해보았다.) 피보나치 수열이란 두 수의 합이 바로 뒤의 수가 되는 수의 배열을 말한다. 왼쪽 사진은 피보나치 수열의 일부를 그림으로 표현한 것인데 저 그림에는 3개의 정사각형이 있다. 한 변의 길이가 a인 정사각형 2개가 만나 그 다음 정사각형의 길이를 설정한다. 즉, 그 다음 정사각형의 길이는 2a가 되는 것이다. 나는 이 수열을 조금 변형시켰는데, 오른쪽 그림에 나타나있다. 한 변의 길이가 a인 정사각형 두 개의 위치를 대각선으로 놓고 그 다음에 올 정사각형의 길이를 두 정사각형의 꼭짓점을 이은 √2로 설정하는 것이다. 따라서 새로 생긴 정사각형과 한 변의 길이가 a인 정사각형의 비율은 √2:1 이다. 이렇게 피보나치 수열을 조금 변형시켜 파빌리온에 사용할 단위체의 위치 배열을 결정했다. 즉, 파빌리온에 3개의 단위체를 사용할 것이며, 가장 아래에 있는 정사각형(단위체)은 지하에, 나머지 두 사각형(단위체)은 지상에 표현하였다.

파빌리온의 전체적인 모습이다. 파빌리온 안으로 들어가면 단위체의 내부만을 볼 수 있도록 하기 위해, 단위체 내부의 패턴을 지하의 계단으로 담아냈다.

파빌리온을 좌측에서 보았을 때 사진이다.

파빌리온의 내부 패턴이 잘 보이도록 찍은 모습이다.

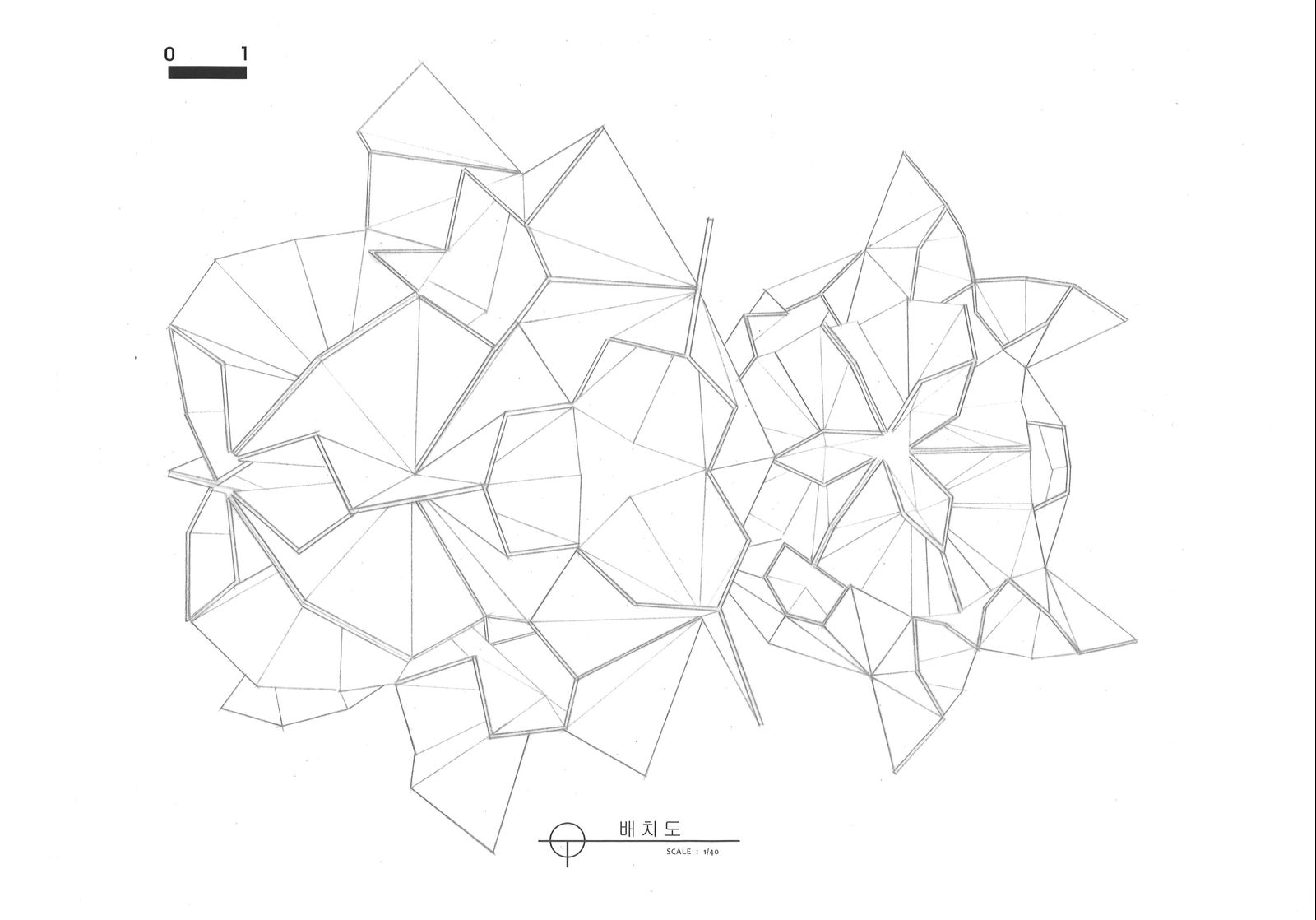
모형을 위에서 바라본 모습이다. 1/40 스케일로 그렸다.

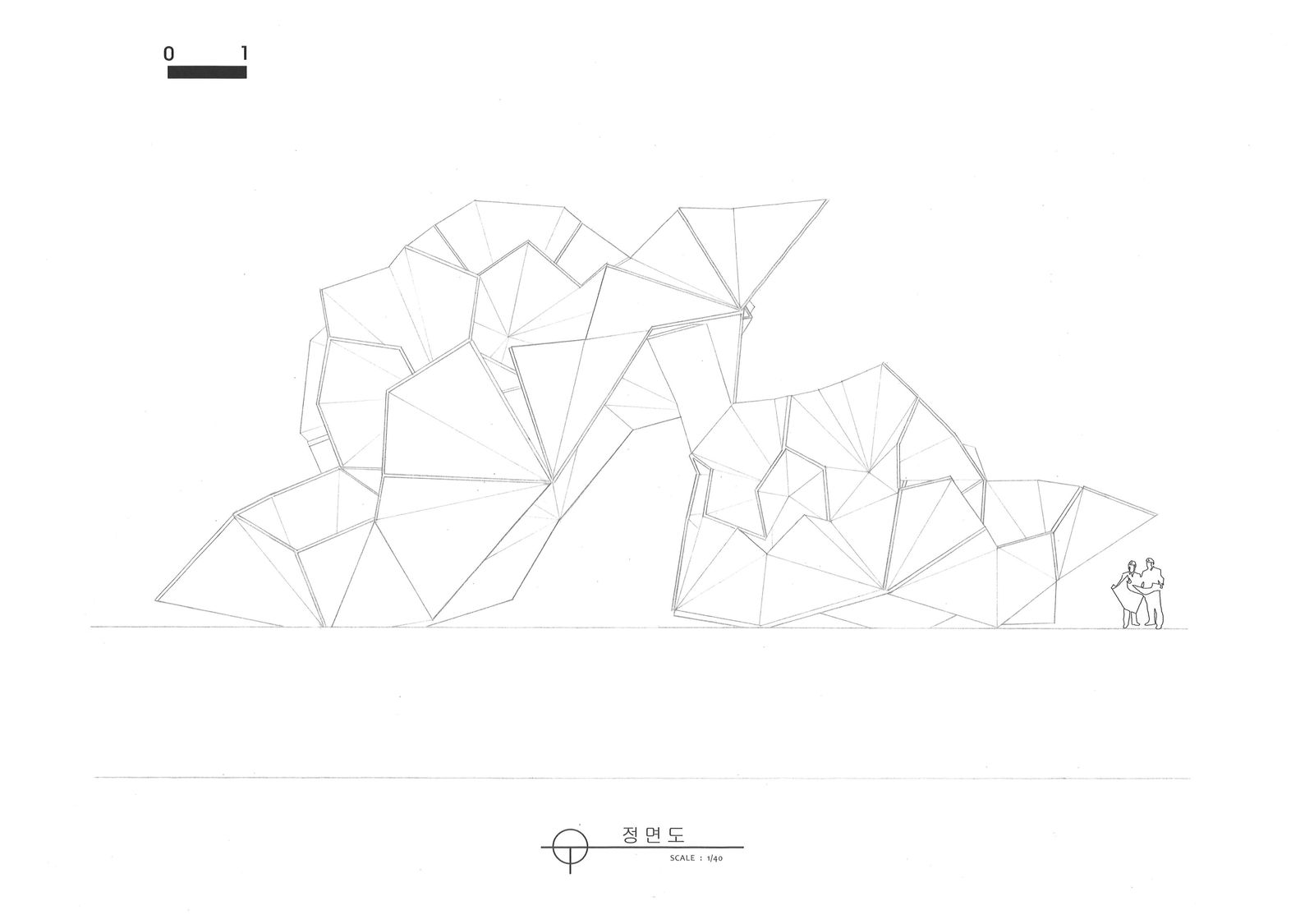
정면에서 바라본 모습이다.

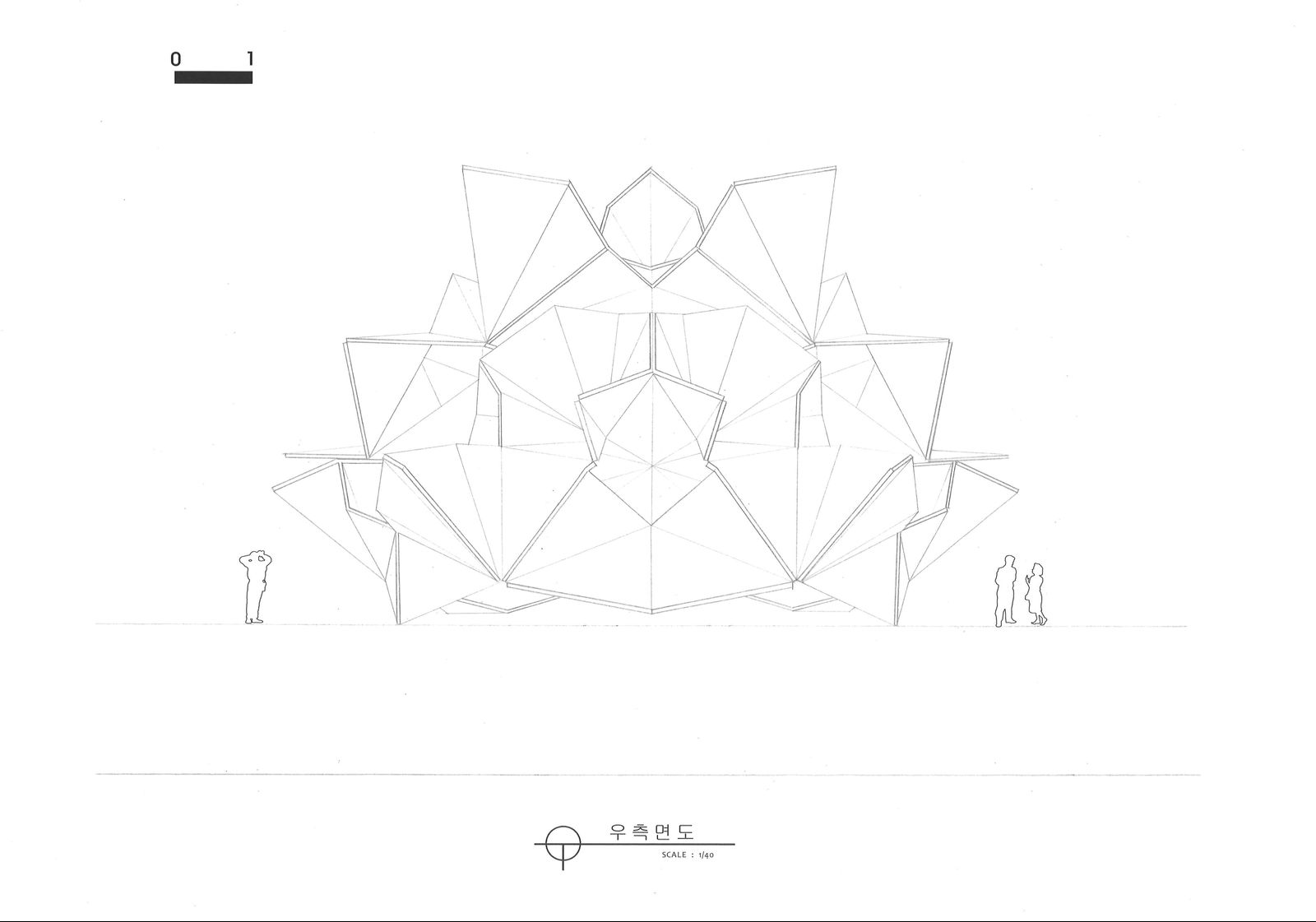
우측에서 바라본 모습이다.